
【題目】若定義在![]() 上的函數
上的函數![]() ,
,![]() .
.
(1)求函數![]() 的單調區間;
的單調區間;
(2)若![]() 、
、![]() 、
、![]() 滿足
滿足![]() ,則稱
,則稱![]() 比
比![]() 更接近
更接近![]() .當
.當![]() ,試比較
,試比較![]() 和
和![]() 哪個更接近
哪個更接近![]() ,并說明理由.
,并說明理由.
 導學全程練創優訓練系列答案
導學全程練創優訓練系列答案科目:高中數學 來源: 題型:
【題目】隨機抽取某中學甲、乙兩班各10名同學,測量他們的身高(單位:cm),獲得身高數據的莖葉圖如圖所示.
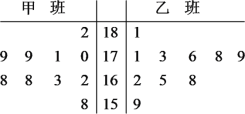
(1)試比較甲、乙兩班分別抽取的這10名同學身高的中位數大小;
(2)現從乙班這10名同學中隨機抽取兩名身高不低于173cm的同學,求身高176cm的同學被抽到的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校為了解本校文、理科學生的學業水平模擬測試數學成績情況,分別從理科班學生中隨機抽取![]() 人的成績得到樣本甲,從文科班學生中隨機抽取
人的成績得到樣本甲,從文科班學生中隨機抽取![]() 人的成績得到樣本乙,根據兩個樣本數據分別得到如下直方圖:
人的成績得到樣本乙,根據兩個樣本數據分別得到如下直方圖:

甲樣本數據直方圖
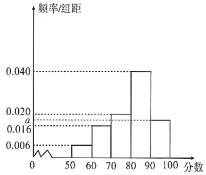
乙樣本數據直方圖
已知乙樣本中數據在![]() 的有
的有![]() 個.
個.
(1)求![]() 和乙樣本直方圖中
和乙樣本直方圖中![]() 的值;
的值;
(2)試估計該校理科班學生本次模擬測試數學成績的平均值和文科班學生本次模擬測試數學成績的中位數(同一組中的數據用該組區間中點值為代表).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某芯片公司為制定下一年的研發投入計劃,需了解年研發資金投入量![]() (單位:億元)對年銷售額
(單位:億元)對年銷售額![]() (單位:億元)的影響.該公司對歷史數據進行對比分析,建立了兩個函數模型:①
(單位:億元)的影響.該公司對歷史數據進行對比分析,建立了兩個函數模型:①![]() ,②
,②![]() ,其中
,其中![]() 均為常數,
均為常數,![]() 為自然對數的底數.
為自然對數的底數.

現該公司收集了近12年的年研發資金投入量![]() 和年銷售額
和年銷售額![]() 的數據,
的數據,![]() ,并對這些數據作了初步處理,得到了右側的散點圖及一些統計量的值.令
,并對這些數據作了初步處理,得到了右側的散點圖及一些統計量的值.令![]()
![]()
![]() ,經計算得如下數據:
,經計算得如下數據:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)設![]() 和
和![]() 的相關系數為
的相關系數為![]() ,
,![]() 和
和![]() 的相關系數為
的相關系數為![]() ,請從相關系數的角度,選擇一個擬合程度更好的模型;
,請從相關系數的角度,選擇一個擬合程度更好的模型;
(2)(i)根據(1的選擇及表中數據,建立![]() 關于
關于![]() 的回歸方程(系數精確到0.01);
的回歸方程(系數精確到0.01);
(ii)若下一年銷售額![]() 需達到90億元,預測下一年的研發資金投入量
需達到90億元,預測下一年的研發資金投入量![]() 是多少億元?
是多少億元?
附:①相關系數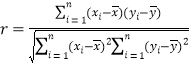 ,回歸直線
,回歸直線![]() 中斜率和截距的最小二乘估計公式分別為:
中斜率和截距的最小二乘估計公式分別為: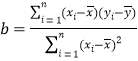 ,
,![]() ;
;
② 參考數據:![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“搜索指數”是網民通過搜索引擎,以每天搜索關鍵詞的次數為基礎所得到的統計指標.“搜索指數”越大,表示網民對該關鍵詞的搜索次數越多,對該關鍵詞相關的信息關注度也越高.下圖是2017年9月到2018年2月這半年中,某個關鍵詞的搜索指數變化的走勢圖.

根據該走勢圖,下列結論正確的是( )
A. 這半年中,網民對該關鍵詞相關的信息關注度呈周期性變化
B. 這半年中,網民對該關鍵詞相關的信息關注度不斷減弱
C. 從網民對該關鍵詞的搜索指數來看,去年10月份的方差小于11月份的方差
D. 從網民對該關鍵詞的搜索指數來看,去年12月份的平均值大于今年1月份的平均值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在衡陽市“創全國文明城市”(簡稱“創文”)活動中,市教育局對本市A,B,C,D四所高中學校按各校人數分層抽樣,隨機抽查了200人,將調查情況進行整理后制成下表:
學校 | A | B | C | D |
抽查人數 | 10 | 15 | 100 | 75 |
“創文”活動中參與的人數 | 9 | 10 | 80 | 49 |
假設每名高中學生是否參與“創文”活動是相互獨立的
(1)若本市共8000名高中學生,估計C學校參與“創文”活動的人數;
(2)在上表中從A,B兩校沒有參與“創文”活動的同學中隨機抽取2人,求恰好A,B兩校各有1人沒有參與“創文”活動的概率;
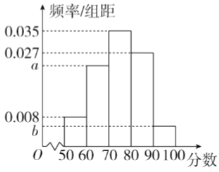
(3)在隨機抽查的200名高中學生中,進行文明素養綜合素質測評(滿分為100分),得到如上的頻率分布直方圖,其中![]() .求a,b的值,并估計參與測評的學生得分的中位數.(計算結果保留兩位小數).
.求a,b的值,并估計參與測評的學生得分的中位數.(計算結果保留兩位小數).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() ,
,![]() ,
,![]() ),
),![]() 和
和![]() 是函數
是函數![]() 的圖象與
的圖象與![]() 軸的2個相鄰交點的橫坐標,且當
軸的2個相鄰交點的橫坐標,且當![]() 時,
時,![]() 取得最大值2.
取得最大值2.
(1)求![]() ,
,![]() ,
,![]() 的值;
的值;
(2)將函數![]() 的圖象上的每一點的橫坐標變為原來的
的圖象上的每一點的橫坐標變為原來的![]() 倍(縱坐標不變),得到函數
倍(縱坐標不變),得到函數![]() 的圖象,再將函數
的圖象,再將函數![]() 的圖象向右平移
的圖象向右平移![]() 個單位,得到函數
個單位,得到函數![]() 的圖象,求函數
的圖象,求函數![]() 在區間
在區間![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com