
【題目】如圖,正三棱柱![]() 所有棱長都是2,D棱AC的中點,E是
所有棱長都是2,D棱AC的中點,E是![]() 棱的中點,AE交
棱的中點,AE交![]() 于點H.
于點H.
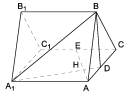
(1)求證:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)求點![]() 到平面
到平面![]() 的距離.
的距離.
【答案】(1)參考解析;(2) ![]() ;(3)
;(3) ![]()
【解析】
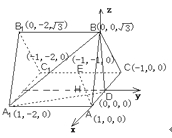
試題分析:(1)由正三棱柱![]() ,可得平面ACB⊥平面
,可得平面ACB⊥平面![]() .又DB⊥AC.所以如圖建立空間直角坐標系.分別點A,E,B,D,
.又DB⊥AC.所以如圖建立空間直角坐標系.分別點A,E,B,D, ![]() 的坐標,得出相應的向量.即可得到向量AE與向量BD,向量
的坐標,得出相應的向量.即可得到向量AE與向量BD,向量![]() 的數量積為零.即可得直線
的數量積為零.即可得直線![]() 平面
平面![]() .
.
(2)由平面![]() ,平面
,平面![]() 分別求出這兩個平面的法向量,根據法向量的夾角得到二面角
分別求出這兩個平面的法向量,根據法向量的夾角得到二面角![]() 的余弦值(根據圖形取銳角).
的余弦值(根據圖形取銳角).
(3)點到平面的距離,轉化為直線與法向量的關系,再通過解三角形的知識即可得點到平面的距離.本小題關鍵是應用解三角形的知識.
試題解析:(1)證明:建立如圖所示, ![]()
![]() ∵
∵![]()
![]()
∴![]() 即AE⊥A1D, AE⊥BD
即AE⊥A1D, AE⊥BD
∴AE⊥面A1BD
(2)由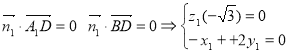 ∴取
∴取![]()
設面AA1B的法向量為 ![]()
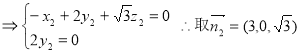 ,
, ![]()
由圖可知二面角D—BA1—A的余弦值為 ![]()
(3)![]() ,平面A1BD的法向量取
,平面A1BD的法向量取![]()
則B1到平面A1BD的距離d=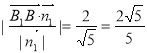


科目:高中數學 來源: 題型:
【題目】寫出由下列各組命題構成的“p或q”“p且q”以及“非p”形式的命題,并判斷它們的真假:
(1)p:3是素數,q:3是偶數;
(2)p:x=-2是方程x2+x-2=0的解,q:x=1是方程x2+x-2=0的解.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】解答
(1)已知全集U={x|﹣5≤x≤10,x∈Z},集合M={x|0≤x≤7,x∈Z},N={x|﹣2≤x<4,x∈Z},求(UN)∩M(分別用描述法和列舉法表示結果)
(2)已知全集U=A∪B={0,1,2,3,4,5,6,7,8,9,10},若集合A∩UB={2,4,6,8},求集合B;
(3)已知集合P={x|ax2+2ax+1=0,a∈R,x∈R},當集合P只有一個元素時,求實數a的值,并求出這個元素.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,命題
,命題![]() 橢圓C1:
橢圓C1: ![]() 表示的是焦點在
表示的是焦點在![]() 軸上的橢圓,命題
軸上的橢圓,命題![]() 對
對![]() ,直線
,直線![]() 與橢圓C2:
與橢圓C2: ![]() 恒有公共點.
恒有公共點.
(1)若命題“![]() ”是假命題,命題“
”是假命題,命題“![]() ”是真命題,求實數
”是真命題,求實數![]() 的取值范圍.
的取值范圍.
(2)若![]() 真
真![]() 假時,求橢圓C1、橢圓C2的上焦點之間的距離d的范圍。
假時,求橢圓C1、橢圓C2的上焦點之間的距離d的范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】等腰直角三角形ABC的直角頂點A在x軸的正半軸上,B在y軸的正半軸上,C在第一象限,設∠BAO=θ(O為坐標原點),AB=AC=2,當OC的長取得最大值時,tanθ的值為( )
A.![]()
B.﹣1+ ![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
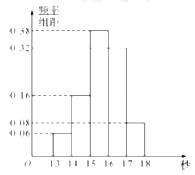
【題目】某班50名學生在一次百米測試中,成績全部介于13秒與18秒之間,將測試結果按如下方式分成五組:第一組![]() ,第二組
,第二組![]() ,…,第五組
,…,第五組![]() ,如圖是按上述分組方法得到的頻率分布直方圖.
,如圖是按上述分組方法得到的頻率分布直方圖.
(Ⅰ)根據頻率分布直方圖,估計這50名學生百米測試成績的中位數和平均數(精確到0.1).
(Ⅱ)若從第一、五組中隨機取出三名學生成績,設取自第一組的個數為![]() ,求
,求![]() 的分布列,期望及方差.
的分布列,期望及方差.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知△ABC的角A、B、C所對的邊分別是a、b、c,設向量 ![]() ,
, ![]() ,
, ![]() .
.
(1)若 ![]() ∥
∥ ![]() ,求證:△ABC為等腰三角形;
,求證:△ABC為等腰三角形;
(2)若 ![]() ⊥
⊥ ![]() ,邊長c=2,角C=
,邊長c=2,角C= ![]() ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com