【題目】在直三棱柱
中， 
,點
分別為
的中點.
（1）求證： 
平面
；
（2）求三棱錐
的體積（錐體的體積公式
，其中
為底面面積， 
為高）
【答案】（1）見解析（2）
【解析】試題分析：（1）欲證
平面
，即證MN∥AC′；（2）利用VA′﹣MNC=VN﹣A′MC=
VN﹣A′BC=
VA′﹣NBC，求三棱錐A′﹣MNC的體積．
試題解析：
（1）
連接AB′，AC′，由已知∠BAC=90°，AB=AC，三棱柱ABC-A′B′C′為直三棱柱，
所以M為AB′的中點，又因為N為B′C′中點，所以MN∥AC′，
又MN平面A′ACC′，AC′平面A′ACC′，所以MN∥平面A′ACC′；
（2）連結BN，由題意A′N⊥B′C′，
∵平面A′B′C′∩平面B′BCC′=B′C′，
∴A′N⊥平面NBC
又A′N=
B′C′=1，
故VA′﹣MNC=VN﹣A′MC=VN﹣A′BC=VA′﹣NBC=
．
口算能手系列答案科目：高中數學 來源： 題型：
【題目】已知
，直線
： 
，橢圓
： 
， 
、
分別為橢圓
的左、右焦點．
（1）當直線
過右焦點
時，求直線
的方程；
（2）設直線
與橢圓
交于
， 
兩點， 
， 
的重心分別為
， 
，若原點
在以線段
為直徑的圓內，求實數
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，正三棱柱
所有棱長都是2，D棱AC的中點，E是
棱的中點，AE交
于點H.
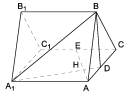
（1）求證：
平面
；
（2）求二面角
的余弦值；
（3）求點
到平面
的距離.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，某地一天中6時至14時的溫度變化曲線近似滿足函數y=Asin（ωx+φ）+B（其中 
），那么這一天6時至14時溫差的最大值是°C；與圖中曲線對應的函數解析式是 ．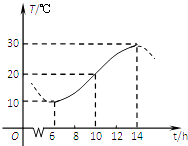 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐
中，平面PAD⊥平面ABCD，PA⊥PD，PA=PD，AB⊥AD，AB=1，AD=2， 
.
（1）求證：PD⊥平面PAB；
（2）求直線PB與平面PCD所成角的正弦值.
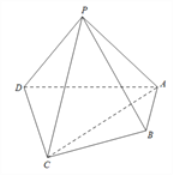
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列4個命題，其中正確的命題序號為（ ）
①|x+ 
|的最小值是2 ② 
的最小值是2 ③log2x+logx2的最小值是2 ④3x+3﹣x的最小值是2．
A.①②③
B.①②④
C.②③④
D.①③④
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在等腰梯形
中， 
， 
， 
，四邊形
為矩形， 
，平面
平面
，點
為線段
中點．
（Ⅰ）求異面直線
與
所成的角的正切值；
（Ⅱ）求證：平面
平面
；
（Ⅲ）求直線
與平面
所成角的正弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖是一個正方體的展開圖，如果將它還原為正方體，那么NC、DE、AF、BM這四條線段所在的直線是異面直線的有多少對？試以其中一對為例進行證明．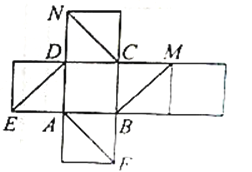
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
