
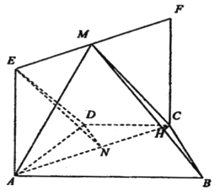
【題目】如圖,在等腰梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,四邊形
,四邊形![]() 為矩形,
為矩形, ![]() ,平面
,平面![]() 平面
平面![]() ,點
,點![]() 為線段
為線段![]() 中點.
中點.

(Ⅰ)求異面直線![]() 與
與![]() 所成的角的正切值;
所成的角的正切值;
(Ⅱ)求證:平面![]() 平面
平面![]() ;
;
(Ⅲ)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)見解析(2)![]()
【解析】【試題分析】(1)借助異面直線所成角的定義找出角,再運用解三角形的知識求解;(2)依據題設線面垂直\面面垂直的判定定理推證;(3)借助線面角的定義先找出線面角,再運用解直角三角形求解:
(Ⅰ)解:取![]() 的中點
的中點![]() ,連接
,連接![]() ,
, ![]() .
.
∵四邊形![]() 為矩形,
為矩形, ![]() 為線段
為線段![]() 中點,
中點,
∴![]() 且
且![]() ,
,
∴![]() ,
,
∴![]() 為異面直線
為異面直線![]() 與
與![]() 所成的角.
所成的角.
在![]() 中,
中, ![]() ,
, ![]() ,
,
∴![]() 且
且![]() ,
,
又∵平面![]()
![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() .
.
在![]() 中,
中, ![]() ,
, ![]() .
.
(Ⅱ)證明:在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
,
又∵平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() .
.
在矩形![]() 中,∵
中,∵![]() ,
, ![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() 平面
平面![]() ,
,
又∵![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(Ⅲ)過點![]() 作
作![]() ,
,
由第(Ⅱ)問知平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() 為直線
為直線![]() 與平面
與平面![]() 所成的角.
所成的角.
在![]() 中,
中, ![]() ,
, ![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() .
.


科目:高中數學 來源: 題型:
【題目】解答
(1)已知全集U={x|﹣5≤x≤10,x∈Z},集合M={x|0≤x≤7,x∈Z},N={x|﹣2≤x<4,x∈Z},求(UN)∩M(分別用描述法和列舉法表示結果)
(2)已知全集U=A∪B={0,1,2,3,4,5,6,7,8,9,10},若集合A∩UB={2,4,6,8},求集合B;
(3)已知集合P={x|ax2+2ax+1=0,a∈R,x∈R},當集合P只有一個元素時,求實數a的值,并求出這個元素.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為評估兩套促銷活動方案(方案1運作費用為5元/件;方案2的運作費用為2元/件),在某地區部分營銷網點進行試點(每個試點網點只采用一種促銷活動方案),運作一年后,對比該地區上一年度的銷售情況,制作相應的等高條形圖如圖所示.
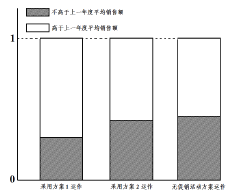
(1)請根據等高條形圖提供的信息,為該公司今年選擇一套較為有利的促銷活動方案(不必說明理由);
(2)已知該公司產品的成本為10元/件(未包括促銷活動運作費用),為制定本年度該地區的產品銷售價格,統計上一年度的8組售價![]() (單位:元/件,整數)和銷量
(單位:元/件,整數)和銷量![]() (單位:件)(
(單位:件)(![]() )如下表所示:
)如下表所示:
售價 | 33 | 35 | 37 | 39 | 41 | 43 | 45 | 47 |
銷量 | 840 | 800 | 740 | 695 | 640 | 580 | 525 | 460 |
①請根據下列數據計算相應的相關指數![]() ,并根據計算結果,選擇合適的回歸模型進行擬合;
,并根據計算結果,選擇合適的回歸模型進行擬合;
②根據所選回歸模型,分析售價![]() 定為多少時?利潤
定為多少時?利潤![]() 可以達到最大.
可以達到最大.
|
|
| |
| 49428.74 | 11512.43 | 175.26 |
| 124650 | ||
(附:相關指數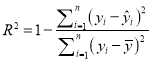 )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,已知中心在原點,離心率為
中,已知中心在原點,離心率為![]() 的橢圓
的橢圓![]() 的一個焦點為圓
的一個焦點為圓![]() :
: ![]() 的圓心.
的圓心.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)設![]() 是橢圓
是橢圓![]() 上一點,過
上一點,過![]() 作兩條斜率之積為
作兩條斜率之積為![]() 的直線
的直線![]() ,
, ![]() ,當直線
,當直線![]() ,
, ![]() 都與圓
都與圓![]() 相切時,求
相切時,求![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知△ABC的角A、B、C所對的邊分別是a、b、c,設向量 ![]() ,
, ![]() ,
, ![]() .
.
(1)若 ![]() ∥
∥ ![]() ,求證:△ABC為等腰三角形;
,求證:△ABC為等腰三角形;
(2)若 ![]() ⊥
⊥ ![]() ,邊長c=2,角C=
,邊長c=2,角C= ![]() ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 的前
的前![]() 項和為
項和為![]() ,且
,且![]() (
(![]() ).
).
(1)求![]() 的通項公式;
的通項公式;
(2)設![]() ,
, ![]() ,
, ![]() 是數列
是數列![]() 的前
的前![]() 項和,求正整數
項和,求正整數![]() ,使得對任意
,使得對任意![]() 均有
均有![]() 恒成立;
恒成立;
(3)設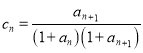 ,
, ![]() 是數列
是數列![]() 的前
的前![]() 項和,若對任意
項和,若對任意![]() 均有
均有![]() 恒成立,求
恒成立,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,設角A,B,C的對邊分別為a,b,c,向量![]() =(cosA,sinA),
=(cosA,sinA),![]() =(
=(![]() ﹣sinA,cosA),若
﹣sinA,cosA),若![]()
![]() =1.
=1.
(1)求角A的大小;
(2)若b=4![]() , 且c=
, 且c=![]() a,求△ABC的面積.
a,求△ABC的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com