
【題目】已知![]() ,命題
,命題![]() 橢圓C1:
橢圓C1: ![]() 表示的是焦點在
表示的是焦點在![]() 軸上的橢圓,命題
軸上的橢圓,命題![]() 對
對![]() ,直線
,直線![]() 與橢圓C2:
與橢圓C2: ![]() 恒有公共點.
恒有公共點.
(1)若命題“![]() ”是假命題,命題“
”是假命題,命題“![]() ”是真命題,求實數
”是真命題,求實數![]() 的取值范圍.
的取值范圍.
(2)若![]() 真
真![]() 假時,求橢圓C1、橢圓C2的上焦點之間的距離d的范圍。
假時,求橢圓C1、橢圓C2的上焦點之間的距離d的范圍。
【答案】(1)![]() ;(2)
;(2)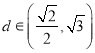 .
.
【解析】試題分析:(1)當命題P為真命題時可得![]() ,當
,當![]() 為真命題時
為真命題時![]() ;由“
;由“![]() ”假,“
”假,“![]() ”真可得
”真可得![]() 一真一假,分兩種情況討論可得結論;(2)由條件知求當
一真一假,分兩種情況討論可得結論;(2)由條件知求當![]() 時,求點
時,求點![]() 與點
與點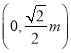 之間距離的最小值,利用函數的知識可求解。
之間距離的最小值,利用函數的知識可求解。
試題解析:
(1)若命題P為真命題時,則有 ![]() ,
,
∵直線![]() 過定點
過定點![]() ,
,
∴當命題![]() 為真命題時,則有
為真命題時,則有![]() ,
,
解得![]() ,
,
∵命題 “![]() ”是假命題,命題 “
”是假命題,命題 “![]() ”是真命題,
”是真命題,
∴命題![]() 和命題
和命題![]() 一真一假。
一真一假。
①當![]() 真
真![]() 假時,
假時,
則有![]() ,解得
,解得![]() ;
;
②當![]() 假
假![]() 真時,
真時,
則有![]() ,解得
,解得![]() 或
或![]() 。
。
綜上所述![]() 或
或![]() 或
或![]() ,
,
所以實數![]() 的取值范圍為
的取值范圍為![]() 。
。
(2)由(1)知當![]() 真
真![]() 假時,可得
假時,可得![]() ,
,
由題意得橢圓![]() 上焦點為
上焦點為![]() ,橢圓
,橢圓![]() 的上焦點為
的上焦點為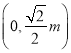 ,
,
所以兩焦點之間的距離![]() ,
,
設![]() ,
, ![]() ,
,
則![]() 在
在![]() 上單調遞減,
上單調遞減,
所以![]() ,即
,即![]() 。
。
所以d的取值范圍為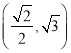 。
。


 作業輔導系列答案
作業輔導系列答案 同步學典一課多練系列答案
同步學典一課多練系列答案 經典密卷系列答案
經典密卷系列答案 金牌課堂練系列答案
金牌課堂練系列答案科目:高中數學 來源: 題型:
【題目】已知命題:“x∈{x|-1≤x≤1},都有不等式x2-x-m<0成立”是真命題.
(1)求實數m的取值集合B;
(2)設不等式(x-3a)(x-a-2)<0的解集為A,若x∈A是x∈B的充分不必要條件,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() (x≠0).
(x≠0).
(1)證明函數f(x)為奇函數;
(2)判斷函數f(x)在[1,+∞)上的單調性,并說明理由;
(3)若x∈[﹣2,﹣3],求函數的最大值和最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
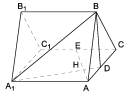
【題目】如圖,正三棱柱![]() 所有棱長都是2,D棱AC的中點,E是
所有棱長都是2,D棱AC的中點,E是![]() 棱的中點,AE交
棱的中點,AE交![]() 于點H.
于點H.
(1)求證:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)求點![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
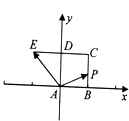
【題目】如圖,已知正方形ABCD的邊長為1,E在CD延長線上,且DE=CD.動點P從點A出發沿正方形ABCD的邊按逆進針方向運動一周回到A點,其中 ![]() =λ
=λ ![]() +μ
+μ ![]() ,則下列命題正確的是 . (填上所有正確命題的序號)
,則下列命題正確的是 . (填上所有正確命題的序號)
①當點P為AD中點時,λ+μ=1;
②λ+μ的最大值為3;
③若y為給定的正數,則一存在向量 ![]() 和實數x,使
和實數x,使 ![]() =x
=x ![]() +y
+y ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某地一天中6時至14時的溫度變化曲線近似滿足函數y=Asin(ωx+φ)+B(其中 ![]() ),那么這一天6時至14時溫差的最大值是°C;與圖中曲線對應的函數解析式是 .
),那么這一天6時至14時溫差的最大值是°C;與圖中曲線對應的函數解析式是 . 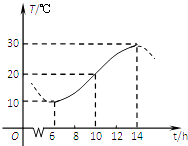
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下表提供了某廠節能降耗技術改造后生產甲產品過程中記錄的產量(![]() 噸)與相應的生產能耗
噸)與相應的生產能耗![]() (噸)標準煤的幾組對照數據:
(噸)標準煤的幾組對照數據:
| 1 | 2 | 3 | 4 | 5 |
| 2 | 3 | 6 | 9 | 10 |
(1)請畫出上表數據的散點圖;
(2)請根據上表提供的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(3)已知該廠技術改造前100噸甲產品能耗為200噸標準煤,試根據(2)求出的線性回歸方程,預測生產100噸甲產品的生產能耗比技術改造前降低多少噸標準煤?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com