
分析 (1)求出函數的定義域,利用奇函數的定義證明即可;
(2)求出a,利用函數單調性的定義進行證明.
解答 解:(1)f(x)為奇函數,其的定義域為(-∞,0)∪(0,+∞).
證明:∵$f({-x})=\frac{{{x^2}+a}}{-x}=-\frac{{{x^2}+a}}{x}=-f(x)$,∴f(x)為奇函數.
(2)證明:由f(1)=2,得a=1.取${x_2}>{x_1}>1,f(x)=\frac{{{x^2}+1}}{x}=x+\frac{1}{x}$,$f({x_1})-f({x_2})={x_1}+\frac{1}{x_1}-({{x_2}+\frac{1}{x_2}})=({{x_1}-{x_2}})\frac{{{x_1}{x_2}-1}}{{{x_1}{x_2}}}$,
∵x1-x2<0,x1x2>1,
∴f(x1)-f(x2)<0,
∴f(x)在(1,+∞)上是增函數.
點評 本題考查函數的奇偶性與單調性,考查學生分析解決問題的能力,屬于中檔題.


科目:高中數學 來源: 題型:解答題
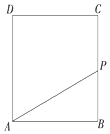 如圖所示,動點P從邊長為1的正方形ABCD的頂點A出發,順次經過頂點B,C,D再回到A.設x表示P點的路程,y表示PA的長度,求y關于x的函數關系式.
如圖所示,動點P從邊長為1的正方形ABCD的頂點A出發,順次經過頂點B,C,D再回到A.設x表示P點的路程,y表示PA的長度,求y關于x的函數關系式.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
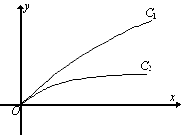 如圖,當參數λ=λ1,λ2時,連續函數y=$\frac{x}{1+λx}$(x≥0)的圖象分別對應曲線C1和C2,則( )
如圖,當參數λ=λ1,λ2時,連續函數y=$\frac{x}{1+λx}$(x≥0)的圖象分別對應曲線C1和C2,則( )| A. | 0<λ2<λ1 | B. | λ2<λ1<0 | C. | λ1<λ2<0 | D. | 0<λ1<λ2 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com