
分析 (1)由{an}為單調遞減數列,可得逆序數為99+98+…+1.
(2)當n為奇數時,a1>a3>…>a2n-1>0.當n為偶數時:0>a2>a4>…>a2n.可得逆序數.
(3)在數列a1,a2,…an中,若a1與后面n-1個數構成p1個逆序對,則有(n-1)-p1不構成逆序對,可得在數列an,an-1,…a1中,逆序數為(n-1)-p1+(n-2)-p2+…+(n-n)-pn.
解答 解:(1)∵{an}為單調遞減數列,∴逆序數為$99+98+…+1=\frac{(99+1)×99}{2}=4950$.
(2)當n為奇數時,a1>a3>…>a2n-1>0.
當n為偶數時:
$\begin{array}{l}{a_n}-{a_{n-2}}=-\frac{n}{n+1}+\frac{n-2}{n-1}(n≥4)\\=\frac{-2}{{{n^2}-1}}\\=\frac{-2}{(n+1)(n-1)}<0\end{array}$
∴0>a2>a4>…>a2n.
當k為奇數時,逆序數為$(k-1)+(k-3)+…+2+\frac{k-3}{2}+\frac{k-5}{2}+…+1=\frac{{3{k^2}-4k+1}}{8}$;
當k為偶數時,逆序數為$(k-1)+(k-3)+…+1+\frac{k-2}{2}+\frac{k-4}{2}+…+1=\frac{{3{k^2}-2k}}{8}$.
(3)在數列a1,a2,…an中,若a1與后面n-1個數構成p1個逆序對,
則有(n-1)-p1不構成逆序對,所以在數列an,an-1,…a1中,
逆序數為$(n-1)-{p_1}+(n-2)-{p_2}+…+(n-n)-{p_n}=\frac{n(n-1)}{2}-a$.
點評 本題考查了等差數列的通項公式與求和公式、新定義逆序數,考查了分類討論方法、推理能力與計算能力,屬于中檔題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $[\frac{1}{2},1]$ | B. | $(\frac{1}{2},1]$ | C. | $(\frac{1}{2},{log_3}2]$ | D. | $[\frac{1}{2},{log_3}2]$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
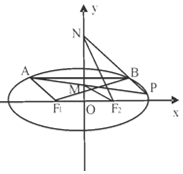 如圖,F1,F2分別是橢圓C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦點,且焦距為2$\sqrt{2}$,動弦AB平行于x軸,且|F1A|+|F1B|=4.
如圖,F1,F2分別是橢圓C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦點,且焦距為2$\sqrt{2}$,動弦AB平行于x軸,且|F1A|+|F1B|=4.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com