
分析 如圖建立直角坐標(biāo)系,設(shè)BF=k,k∈[0,3].得F(2-$\frac{1}{2}k$,$\frac{\sqrt{3}}{2}k$),E($\frac{3}{2}-\frac{1}{2}k$,$\frac{\sqrt{3}}{2}(k+1)$).
tan∠EAB=$\frac{\sqrt{3}(k+1)}{3-k}$,tan∠FAB=$\frac{\sqrt{3}k}{4-k}$,.tanθ=tan(∠EAB-∠FAB)=$\frac{\sqrt{3}}{{k}^{2}-k+3}$;即可求取值范圍.
解答 解:如圖建立直角坐標(biāo)系,設(shè)BF=k,k∈[0,3].
∴∠B=60°,∴F(2-$\frac{1}{2}k$,$\frac{\sqrt{3}}{2}k$),E($\frac{3}{2}-\frac{1}{2}k$,$\frac{\sqrt{3}}{2}(k+1)$).
∴tan∠EAB=$\frac{\sqrt{3}(k+1)}{3-k}$,tan∠FAB=$\frac{\sqrt{3}k}{4-k}$,.
tanθ=tan(∠EAB-∠FAB)=$\frac{\sqrt{3}}{{k}^{2}-k+3}$;
∵k∈[0,3].∴${k}^{2}-k+3∈[\frac{11}{4},9]$,tanθ的取值范圍是[$\frac{\sqrt{3}}{9},\frac{4\sqrt{3}}{11}$]
故答案為[$\frac{\sqrt{3}}{9},\frac{4\sqrt{3}}{11}$].
點(diǎn)評(píng) 本題考查了建立坐標(biāo)系解決平面幾何問(wèn)題,屬于難題.


 閱讀快車系列答案
閱讀快車系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | (1,5) | B. | [2,5) | C. | (1,2] | D. | [2,+∞) |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
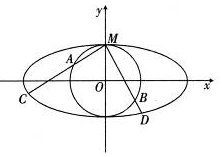 如圖,圓O(O為坐標(biāo)原點(diǎn))與離心率為$\frac{{\sqrt{3}}}{2}$的橢圓T:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)相交于點(diǎn)M(0,1).
如圖,圓O(O為坐標(biāo)原點(diǎn))與離心率為$\frac{{\sqrt{3}}}{2}$的橢圓T:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)相交于點(diǎn)M(0,1). 查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | $\frac{3\sqrt{3}π}{8}$ | B. | $\frac{3\sqrt{3}π}{7}$ | C. | $\frac{3\sqrt{2}π}{8}$ | D. | $\frac{3\sqrt{2}π}{7}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com