
分析 (1)利用分離常數法轉化為二次函數求函數的值域.
(2)利用配方求二次函數來求函數的值域.
解答 解:(1)y=$\frac{1-{x}^{2}}{1+{x}^{2}}$;
化簡:y=$\frac{1-{x}^{2}}{1+{x}^{2}}$=$\frac{2-(1+{x}^{2})}{1+{x}^{2}}$=-1$+\frac{2}{1+{x}^{2}}$
∵1+x2≥1,
∴$0<\frac{2}{{x}^{2}+1}≤2$
故得函數y的范圍是-1<y≤1,即函數的值域為(-1,1].
(2)y=$\sqrt{-2{x}^{2}+x+3}$.
∵-2x2+x+3≥0,
∴y≥0
∵-2x2+x+3=$-2(x-\frac{1}{2})^{2}+\frac{25}{8}$$≤\frac{25}{8}$
∴y≤$\sqrt{\frac{25}{8}}$=$\frac{5\sqrt{2}}{4}$
故得函數y的范圍是0≤y≤$\frac{5\sqrt{2}}{4}$,即函數的值域為[0,$\frac{5\sqrt{2}}{4}$].
點評 本題考查了函數值域的求法.高中函數值域求法有:1、觀察法,2、配方法,3、反函數法,4、判別式法;5、換元法,6、數形結合法,7、不等式法,8、分離常數法,9、單調性法,10、利用導數求函數的值域,11、最值法,12、構造法,13、比例法.要根據題意選擇.


 期末好成績系列答案
期末好成績系列答案 99加1領先期末特訓卷系列答案
99加1領先期末特訓卷系列答案 百強名校期末沖刺100分系列答案
百強名校期末沖刺100分系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 10π | B. | 4π | C. | 16π | D. | 8π |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -14 | B. | -9 | C. | -5 | D. | -1 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
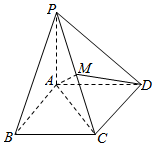 已知四棱錐P-ABCD中,底面為矩形,PA⊥底面ABCD,PA=BC=1,AB=2,M為PC上一點,且BP⊥平面ADM.
已知四棱錐P-ABCD中,底面為矩形,PA⊥底面ABCD,PA=BC=1,AB=2,M為PC上一點,且BP⊥平面ADM.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com