
| A. | 4 | B. | -4 | C. | -3 | D. | 3 |
分析 運用正弦定理,把邊化成角得到sinA=3sinBsinC,再與條件cosA=3cosBcosC相減,運用兩角和的余弦公式,再用誘導公式轉化為cosA,由同角公式,即可求出tanA.
解答 解:∵a=3bsinC,
由正弦定理得:sinA=3sinBsinC①,
又cosA=3cosBcosC②,
②-①得,cosA-sinA=3(cosBcosC-sinBsinC)
=3cos(B+C)=-3cosA,
∴sinA=4cosA,
∴tanA=$\frac{sinA}{cosA}$=4.
故選:A.
點評 本題主要考查解三角形中的正弦定理及應用,同時考查兩角和差的余弦公式,誘導公式,以及同角三角函數的關系式,這些都是三角中的基本公式,務必要掌握,注意公式的逆用.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
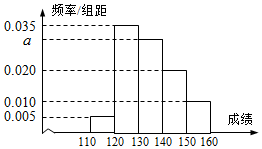 從高三年級隨機抽取200名學生,將他們的某次考試數學成績繪制成頻率分布直方圖.由圖中數據可知成績在[130,140)內的學生人數為60.
從高三年級隨機抽取200名學生,將他們的某次考試數學成績繪制成頻率分布直方圖.由圖中數據可知成績在[130,140)內的學生人數為60.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com