
分析 先判斷函數g(x)的取值范圍,然后根據ff(x)>0或g(x)>0.則可以求出m的取值范圍.
解答 解:g(x)=2x-2>0則x>1,
又∵?x∈R,都有f(x)>0或g(x)>0,
∴f(x)=m(x-2m)(x+m-3)>0在x≤1時恒成立,
即m(x-2m)(x+m+3)>0在x≤1時恒成立,
則二次函數y=m(x-2m)(x+m-3)圖象開口只能向上,且與x軸交點都在(1,0)的右側,
∴$\left\{\begin{array}{l}{m>0}\\{2m>1}\\{3-m>1}\end{array}\right.$,
解得$\frac{1}{2}$<m<2,
故答案為:($\frac{1}{2}$,2)
點評 本題主要考查指數函數和二次函數的圖象和性質,根據條件確定f(x)=m(x-2m)(x+m-3)>0在x≤1時恒成立是解決本題的關鍵,綜合性較強,難度較大.


科目:高中數學 來源: 題型:選擇題
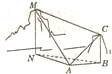 如圖,已知一座山高BC=80米,為了測量另一座山高MN,和兩山頂之間的距離CM,在A點測得M點的仰角∠MAN=60°,C點的仰角∠BAC=30°,C、M兩點的張角∠MAC=60°,從C點測得∠ACM=75°,則MN與CM分別等于多少米( )
如圖,已知一座山高BC=80米,為了測量另一座山高MN,和兩山頂之間的距離CM,在A點測得M點的仰角∠MAN=60°,C點的仰角∠BAC=30°,C、M兩點的張角∠MAC=60°,從C點測得∠ACM=75°,則MN與CM分別等于多少米( )| A. | 40(3+$\sqrt{3}$),140$\sqrt{2}$ | B. | 40(3+$\sqrt{3}$),80$\sqrt{6}$ | C. | 60($\sqrt{2}$+$\sqrt{3}$),140$\sqrt{2}$ | D. | 60($\sqrt{2}$+$\sqrt{3}$),80$\sqrt{6}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 是偶函數,而非奇函數 | B. | 既是奇函數又是偶函數 | ||
| C. | 是奇函數,而非偶函數 | D. | 是非奇非偶函數 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $2\sqrt{3}$ | B. | $3\sqrt{2}$ | C. | 6 | D. | $\sqrt{6}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 奇函數且它的圖象關于點(π,0)對稱 | |
| B. | 奇函數且它的圖象關于點($\frac{3π}{4}$,0)對稱 | |
| C. | 偶函數且它的圖象關于直線x=π對稱 | |
| D. | 偶函數且它的圖象關于直線x=$\frac{3π}{4}$對稱 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 12種 | B. | 16種 | C. | 20種 | D. | 24種 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
 如圖所示,已知正方體(圖1)面對角線長為a,沿對角面將其切割成兩塊,拼成圖2所示的幾何體,那么拼成后的幾何體的全面積為$({2+\sqrt{2}}){a^2}$.
如圖所示,已知正方體(圖1)面對角線長為a,沿對角面將其切割成兩塊,拼成圖2所示的幾何體,那么拼成后的幾何體的全面積為$({2+\sqrt{2}}){a^2}$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com