
| A. | $\sqrt{6}$ | B. | 6 | C. | $\sqrt{2}$ | D. | 2 |
分析 與(2$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$)⊥(-2$\overrightarrow{{e}_{1}}$+3$\overrightarrow{{e}_{2}}$),可得(2$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$)•(-2$\overrightarrow{{e}_{1}}$+3$\overrightarrow{{e}_{2}}$)=0.可得:$\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}$=$\frac{1}{4}$.再利用數量積運算性質即可得出.
解答 解:∵(2$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$)⊥(-2$\overrightarrow{{e}_{1}}$+3$\overrightarrow{{e}_{2}}$),∴(2$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$)•(-2$\overrightarrow{{e}_{1}}$+3$\overrightarrow{{e}_{2}}$)=-4${\overrightarrow{{e}_{1}}}^{2}$+3${\overrightarrow{{e}_{2}}}^{2}$+4$\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}$=-1+4$\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}$=0.
可得:$\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}$=$\frac{1}{4}$.
則|$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$|=$\sqrt{{\overrightarrow{{e}_{1}}}^{2}+4{\overrightarrow{{e}_{2}}}^{2}+4\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}}$=$\sqrt{1+4+4×\frac{1}{4}}$=$\sqrt{6}$.
故選:A.
點評 本題考查了向量垂直與數量積的關系、數量積運算性質,考查了推理能力與計算能力,屬于基礎題.


科目:高中數學 來源: 題型:解答題
 如圖,AB=38米,從點A發出的光線經水平放置于C處的平面鏡(大小忽略不計)反射后過點B,已知AC=10米,BC=42米.
如圖,AB=38米,從點A發出的光線經水平放置于C處的平面鏡(大小忽略不計)反射后過點B,已知AC=10米,BC=42米.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
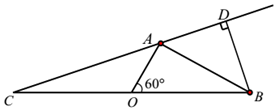 隨著節假日外出旅游人數增多,倡導文明旅游的同時,生活垃圾處理也面臨新的挑戰,某海濱城市沿海有A,B,C三個旅游景點,在岸邊BC兩地的中點處設有一個垃圾回收站點O(如圖),A,B兩地相距10km,從回收站O觀望A地和B地所成的視角為60°,且${\overrightarrow{OA}^2}+{\overrightarrow{OB}^2}≥4\overrightarrow{OA}•\overrightarrow{OB}$,設AC=xkm;
隨著節假日外出旅游人數增多,倡導文明旅游的同時,生活垃圾處理也面臨新的挑戰,某海濱城市沿海有A,B,C三個旅游景點,在岸邊BC兩地的中點處設有一個垃圾回收站點O(如圖),A,B兩地相距10km,從回收站O觀望A地和B地所成的視角為60°,且${\overrightarrow{OA}^2}+{\overrightarrow{OB}^2}≥4\overrightarrow{OA}•\overrightarrow{OB}$,設AC=xkm;查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com