
【題目】如圖,在四棱錐![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
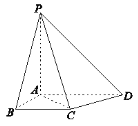
(1)求證:![]() 平面
平面![]() ;
;
(2)在棱![]() 上是否存在點(diǎn)
上是否存在點(diǎn)![]() ,使得
,使得![]() 平面
平面![]() ?若存在,確定點(diǎn)
?若存在,確定點(diǎn)![]() 的位置;若不存在,說(shuō)明理由.
的位置;若不存在,說(shuō)明理由.
【答案】(1)見(jiàn)解析(2)在棱![]() 上存在點(diǎn)
上存在點(diǎn)![]() ,
,![]() ,使得
,使得![]() 平面
平面![]() .
.
【解析】
(1)由題意,利用勾股定理可得![]() ,可得
,可得![]() ,可得
,可得![]() ,利用線面垂直的性質(zhì)可得
,利用線面垂直的性質(zhì)可得![]() ,利用線面垂直的判定定理即可證明DC⊥平面PAC;
,利用線面垂直的判定定理即可證明DC⊥平面PAC;
(2)過(guò)點(diǎn)A作AH⊥PC,垂足為H,由(1)利用線面垂直的判定定理可證明AH⊥平面PCD,在RT△PAC中,由PA=2,![]() ,可求
,可求![]() ,即在棱PC上存在點(diǎn)H,且
,即在棱PC上存在點(diǎn)H,且![]() ,使得AH⊥平面PCD.
,使得AH⊥平面PCD.
解(1)由題意,可得![]() ,
,
∴![]() ,即
,即![]() ,
,
又![]() 底面
底面![]() ,
,
∴![]() ,
,
且![]() ,
,
∴![]() 平面
平面![]() ;
;
(2)過(guò)點(diǎn)![]() 作
作![]() ,垂足為
,垂足為![]() ,
,
由(1)可得![]() ,
,
又![]() ,
,
∴![]() 平面
平面![]() .
.
在![]() 中,∵
中,∵![]() ,
,![]() ,
,![]()
∴![]() .
.
即在棱![]() 上存在點(diǎn)
上存在點(diǎn)![]() ,且
,且![]() ,使得
,使得![]() 平面
平面![]() .
.



 開(kāi)心蛙狀元測(cè)試卷系列答案
開(kāi)心蛙狀元測(cè)試卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某企業(yè)生產(chǎn)甲、乙兩種產(chǎn)品,已知生產(chǎn)每噸甲產(chǎn)品要用A原料3噸,B原料2噸;生產(chǎn)每噸乙產(chǎn)品要用A原料1噸,B原料3噸.銷(xiāo)售每噸甲產(chǎn)品可獲得利潤(rùn)5萬(wàn)元,每噸乙產(chǎn)品可獲得利潤(rùn)3萬(wàn)元.該企業(yè)在一個(gè)生產(chǎn)周期內(nèi)消耗A原料不超過(guò)13噸,B原料不超過(guò)18噸.
(1)列出甲、乙兩種產(chǎn)品滿足的關(guān)系式,并畫(huà)出相應(yīng)的平面區(qū)域;
(2)在一個(gè)生產(chǎn)周期內(nèi)該企業(yè)生產(chǎn)甲、乙兩種產(chǎn)品各多少噸時(shí)可獲得利潤(rùn)最大,最大利潤(rùn)是多少?
(用線性規(guī)劃求解要畫(huà)出規(guī)范的圖形及具體的解答過(guò)程)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】隨著社會(huì)的發(fā)展,終身學(xué)習(xí)成為必要,工人知識(shí)要更新,學(xué)習(xí)培訓(xùn)必不可少,現(xiàn)某工廠有工人1000名,其中250名工人參加短期培訓(xùn)(稱為![]() 類工人),另外750名工人參加過(guò)長(zhǎng)期培訓(xùn)(稱為
類工人),另外750名工人參加過(guò)長(zhǎng)期培訓(xùn)(稱為![]() 類工人),從該工廠的工人中共抽查了100名工人,調(diào)查他們的生產(chǎn)能力(此處生產(chǎn)能力指一天加工的零件數(shù))得到
類工人),從該工廠的工人中共抽查了100名工人,調(diào)查他們的生產(chǎn)能力(此處生產(chǎn)能力指一天加工的零件數(shù))得到![]() 類工人生產(chǎn)能力的莖葉圖(左圖),
類工人生產(chǎn)能力的莖葉圖(左圖),![]() 類工人生產(chǎn)能力的頻率分布直方圖(右圖).
類工人生產(chǎn)能力的頻率分布直方圖(右圖).

(1)問(wèn)![]() 類、
類、![]() 類工人各抽查了多少工人,并求出直方圖中的
類工人各抽查了多少工人,并求出直方圖中的![]() ;
;
(2)求![]() 類工人生產(chǎn)能力的中位數(shù),并估計(jì)
類工人生產(chǎn)能力的中位數(shù),并估計(jì)![]() 類工人生產(chǎn)能力的平均數(shù)(同一組中的數(shù)據(jù)用該組區(qū)間的中點(diǎn)值作代表);
類工人生產(chǎn)能力的平均數(shù)(同一組中的數(shù)據(jù)用該組區(qū)間的中點(diǎn)值作代表);
(3)若規(guī)定生產(chǎn)能力在![]() 內(nèi)為能力優(yōu)秀,由以上統(tǒng)計(jì)數(shù)據(jù)在答題卡上完成下面的
內(nèi)為能力優(yōu)秀,由以上統(tǒng)計(jì)數(shù)據(jù)在答題卡上完成下面的![]() 列聯(lián)表,并判斷是否可以在犯錯(cuò)誤概率不超過(guò)0.1%的前提下,認(rèn)為生產(chǎn)能力與培訓(xùn)時(shí)間長(zhǎng)短有關(guān).能力與培訓(xùn)時(shí)間列聯(lián)表
列聯(lián)表,并判斷是否可以在犯錯(cuò)誤概率不超過(guò)0.1%的前提下,認(rèn)為生產(chǎn)能力與培訓(xùn)時(shí)間長(zhǎng)短有關(guān).能力與培訓(xùn)時(shí)間列聯(lián)表
短期培訓(xùn) | 長(zhǎng)期培訓(xùn) | 合計(jì) | |
能力優(yōu)秀 | |||
能力不優(yōu)秀 | |||
合計(jì) |
參考數(shù)據(jù):
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
參考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】下列說(shuō)法正確的是( )
A.若![]() 為真命題,則
為真命題,則![]() ,
,![]() 均為假命題;
均為假命題;
B.命題“若![]() ,則
,則![]() ”的逆否命題為真命題;
”的逆否命題為真命題;
C.等比數(shù)列![]() 的前
的前![]() 項(xiàng)和為
項(xiàng)和為![]() ,若“
,若“![]() ”則“
”則“![]() ”的否命題為真命題;
”的否命題為真命題;
D.“平面向量![]() 與
與![]() 的夾角為鈍角”的充要條件是“
的夾角為鈍角”的充要條件是“![]() ”
”
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】我國(guó)古代數(shù)學(xué)名著《九章算術(shù)》中記載的“芻甍”(chu meng)是指底面為矩形,頂部只有一條棱的五面體.如圖,五面體![]() 是一個(gè)芻甍,其中
是一個(gè)芻甍,其中![]() 是正三角形,
是正三角形,![]() ,則以下兩個(gè)結(jié)論:①
,則以下兩個(gè)結(jié)論:①![]() ;②
;②![]() ,( )
,( )
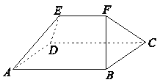
A.①和②都不成立B.①成立,但②不成立
C.①不成立,但②成立D.①和②都成立
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() 為自然對(duì)數(shù)的底數(shù)).
為自然對(duì)數(shù)的底數(shù)).
(1)求函數(shù)![]() 的值域;
的值域;
(2)若不等式![]() 對(duì)任意
對(duì)任意![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(3)證明:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】小明跟父母、爺爺奶奶一同參加《中國(guó)詩(shī)詞大會(huì)》的現(xiàn)場(chǎng)錄制,5人坐成一排.若小明的父母至少有一人與他相鄰,則不同坐法的總數(shù)為
A. 60 B. 72 C. 84 D. 96
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() 時(shí),求
時(shí),求![]() 的最大值;
的最大值;
(2)若函數(shù)![]() 有兩個(gè)零點(diǎn),求
有兩個(gè)零點(diǎn),求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() 為等邊三角形,
為等邊三角形,![]()
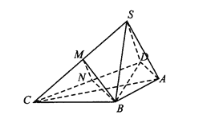
(1)若點(diǎn)![]() 分別是線段
分別是線段![]() 的中點(diǎn),求證:平面
的中點(diǎn),求證:平面![]() 平面
平面![]() ;
;
(2)若二面角![]() 為直二面角,求直線
為直二面角,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com