
【題目】隨著社會的發展,終身學習成為必要,工人知識要更新,學習培訓必不可少,現某工廠有工人1000名,其中250名工人參加短期培訓(稱為![]() 類工人),另外750名工人參加過長期培訓(稱為
類工人),另外750名工人參加過長期培訓(稱為![]() 類工人),從該工廠的工人中共抽查了100名工人,調查他們的生產能力(此處生產能力指一天加工的零件數)得到
類工人),從該工廠的工人中共抽查了100名工人,調查他們的生產能力(此處生產能力指一天加工的零件數)得到![]() 類工人生產能力的莖葉圖(左圖),
類工人生產能力的莖葉圖(左圖),![]() 類工人生產能力的頻率分布直方圖(右圖).
類工人生產能力的頻率分布直方圖(右圖).

(1)問![]() 類、
類、![]() 類工人各抽查了多少工人,并求出直方圖中的
類工人各抽查了多少工人,并求出直方圖中的![]() ;
;
(2)求![]() 類工人生產能力的中位數,并估計
類工人生產能力的中位數,并估計![]() 類工人生產能力的平均數(同一組中的數據用該組區間的中點值作代表);
類工人生產能力的平均數(同一組中的數據用該組區間的中點值作代表);
(3)若規定生產能力在![]() 內為能力優秀,由以上統計數據在答題卡上完成下面的
內為能力優秀,由以上統計數據在答題卡上完成下面的![]() 列聯表,并判斷是否可以在犯錯誤概率不超過0.1%的前提下,認為生產能力與培訓時間長短有關.能力與培訓時間列聯表
列聯表,并判斷是否可以在犯錯誤概率不超過0.1%的前提下,認為生產能力與培訓時間長短有關.能力與培訓時間列聯表
短期培訓 | 長期培訓 | 合計 | |
能力優秀 | |||
能力不優秀 | |||
合計 |
參考數據:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
參考公式:![]() ,其中
,其中![]() .
.
【答案】(1)0.024;(2)可以在犯錯誤概率不超過![]() 的前提下,認為生產能力與培訓時間長短有關
的前提下,認為生產能力與培訓時間長短有關
【解析】試題分析:(1)由莖葉圖知A類工人中抽查人數為25名,B類工人中應抽查100﹣25=75,由頻率分布直方圖求出x;
(2)由莖葉圖知A類工人生產能力的中位數為122,由(1)及頻率分布直方圖,估計B類工人生產能力的平均數;
(3)求出K2,與臨界值比較,即可得出結論.
試題解析:
解:(1)由莖葉圖知A類工人中抽查人數為25名,
∴B類工人中應抽查100-25=75(名).
由頻率分布直方圖得 (0.008+0.02+0.048+x)10=1,得x=0.024.
(2)由莖葉圖知A類工人生產能力的中位數為122
由(1)及頻率分布直方圖,估計B類工人生產能力的平均數為
![]() 1150.00810+1250.02010+1350.04810+1450.02410=133.8
1150.00810+1250.02010+1350.04810+1450.02410=133.8
(3)由(1)及所給數據得能力與培訓的22列聯表,
短期培訓 | 長期培訓 | 合計 | |
能力優秀 | 8 | 54 | 62 |
能力不優秀 | 17 | 21 | 38 |
合計 | 25 | 75 | 100 |
由上表得![]() >10.828
>10.828
因此,可以在犯錯誤概率不超過0.1%的前提下,認為生產能力與培訓時間長短有關.


科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 過點
過點![]() ,其參數方程為
,其參數方程為![]() (
(![]() 為參數,
為參數,![]() ),以
),以![]() 為極點,
為極點,![]() 軸非負半軸為極軸建立極坐標系,曲線
軸非負半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)求已知曲線![]() 和曲線
和曲線![]() 交于
交于![]() 兩點,且
兩點,且![]() ,求實數
,求實數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為菱形,
為菱形, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分別是
分別是![]() ,
, ![]() 的中點.
的中點.

(1)證明: ![]() ;
;
(2)設![]() 為線段
為線段![]() 上的動點,若線段
上的動點,若線段![]() 長的最小值為
長的最小值為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)見解析;(2)![]()
【解析】試題分析:(1)證明線線垂直則需證明線面垂直,根據題意易得![]() ,然后根據等邊三角形的性質可得
,然后根據等邊三角形的性質可得![]() ,又
,又![]() ,因此
,因此![]() 得
得![]() 平面
平面![]() ,從而得證(2)先找到EH什么時候最短,顯然當線段
,從而得證(2)先找到EH什么時候最短,顯然當線段![]() 長的最小時,
長的最小時, ![]() ,在
,在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,∴
,∴![]() ,由
,由![]() 中,
中, ![]() ,
, ![]() ,∴
,∴![]() .然后建立空間直角坐標系,寫出兩個面法向量再根據向量的夾角公式即可得余弦值
.然后建立空間直角坐標系,寫出兩個面法向量再根據向量的夾角公式即可得余弦值
解析:(1)證明:∵四邊形![]() 為菱形,
為菱形, ![]() ,
,
∴![]() 為正三角形.又
為正三角形.又![]() 為
為![]() 的中點,∴
的中點,∴![]() .
.
又![]() ,因此
,因此![]() .
.
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() .
.
而![]() 平面
平面![]() ,
, ![]() 平面
平面![]() 且
且![]() ,
,
∴![]() 平面
平面![]() .又
.又![]() 平面
平面![]() ,∴
,∴![]() .
.

(2)如圖, ![]() 為
為![]() 上任意一點,連接
上任意一點,連接![]() ,
, ![]() .
.

當線段![]() 長的最小時,
長的最小時, ![]() ,由(1)知
,由(1)知![]() ,
,
∴![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,故
,故![]() .
.
在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
,
由![]() 中,
中, ![]() ,
, ![]() ,∴
,∴![]() .
.
由(1)知![]() ,
, ![]() ,
, ![]() 兩兩垂直,以
兩兩垂直,以![]() 為坐標原點,建立如圖所示的空間直角坐標系,又
為坐標原點,建立如圖所示的空間直角坐標系,又![]() ,
, ![]() 分別是
分別是![]() ,
, ![]() 的中點,
的中點,
可得![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, 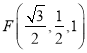 ,
,
所以![]() ,
,  .
.
設平面![]() 的一法向量為
的一法向量為![]() ,
,
則![]() 因此
因此 ,
,
取![]() ,則
,則![]() ,
,
因為![]() ,
, ![]() ,
, ![]() ,所以
,所以![]() 平面
平面![]() ,
,
故![]() 為平面
為平面![]() 的一法向量.又
的一法向量.又![]() ,
,
所以![]()

![]() .
.
易得二面角![]() 為銳角,故所求二面角的余弦值為
為銳角,故所求二面角的余弦值為![]() .
.

【題型】解答題
【結束】
20
【題目】【2018湖北七市(州)教研協作體3月高三聯考】已知橢圓![]() :
: ![]()
![]() 的左頂點為
的左頂點為![]() ,上頂點為
,上頂點為![]() ,直線
,直線![]() 與直線
與直線![]() 垂直,垂足為
垂直,垂足為![]() 點,且點
點,且點![]() 是線段
是線段![]() 的中點.
的中點.

(I)求橢圓![]() 的方程;
的方程;
(II)如圖,若直線![]() :
: ![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
, ![]() 兩點,點
兩點,點![]() 在橢圓
在橢圓![]() 上,且四邊形
上,且四邊形![]() 為平行四邊形,求證:四邊形
為平行四邊形,求證:四邊形![]() 的面積
的面積![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2017吉林延邊州模擬)已知在△ABC中,B(-1,0),C(1,0),且|AB|+|AC|=4.
(1)求動點A的軌跡M的方程;
(2)P為軌跡M上的動點,△PBC的外接圓為☉O1,當點P在軌跡M上運動時,求點O1到x軸的距離的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著社會的發展,終身學習成為必要,工人知識要更新,學習培訓必不可少,現某工廠有工人1000名,其中250名工人參加短期培訓(稱為![]() 類工人),另外750名工人參加過長期培訓(稱為
類工人),另外750名工人參加過長期培訓(稱為![]() 類工人),從該工廠的工人中共抽查了100名工人,調查他們的生產能力(此處生產能力指一天加工的零件數)得到
類工人),從該工廠的工人中共抽查了100名工人,調查他們的生產能力(此處生產能力指一天加工的零件數)得到![]() 類工人生產能力的莖葉圖(左圖),
類工人生產能力的莖葉圖(左圖),![]() 類工人生產能力的頻率分布直方圖(右圖).
類工人生產能力的頻率分布直方圖(右圖).

(1)問![]() 類、
類、![]() 類工人各抽查了多少工人,并求出直方圖中的
類工人各抽查了多少工人,并求出直方圖中的![]() ;
;
(2)求![]() 類工人生產能力的中位數,并估計
類工人生產能力的中位數,并估計![]() 類工人生產能力的平均數(同一組中的數據用該組區間的中點值作代表);
類工人生產能力的平均數(同一組中的數據用該組區間的中點值作代表);
(3)若規定生產能力在![]() 內為能力優秀,由以上統計數據在答題卡上完成下面的
內為能力優秀,由以上統計數據在答題卡上完成下面的![]() 列聯表,并判斷是否可以在犯錯誤概率不超過0.1%的前提下,認為生產能力與培訓時間長短有關.能力與培訓時間列聯表
列聯表,并判斷是否可以在犯錯誤概率不超過0.1%的前提下,認為生產能力與培訓時間長短有關.能力與培訓時間列聯表
短期培訓 | 長期培訓 | 合計 | |
能力優秀 | |||
能力不優秀 | |||
合計 |
參考數據:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
參考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于下列四個命題:
p1:x0∈(0,+∞),![]() ;
;
p2:x0∈(0,1),lo![]() x0>lo
x0>lo![]() x0;
x0;
p3:x∈(0,+∞),![]() <lo
<lo![]() x;
x;
p4:x∈![]() <lo
<lo![]() x.
x.
其中的真命題是( )
A. p1,p3 B. p1,p4
C. p2,p3 D. p2,p4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,以
中,以![]() 為極點,
為極點, ![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的方程是
的方程是![]() ,將
,將![]() 向上平移2個單位得到曲線
向上平移2個單位得到曲線![]() .
.
(1)求曲線![]() 的極坐標方程;
的極坐標方程;
(2)直線![]() 的參數方程為
的參數方程為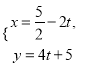 (
(![]() 為參數),判斷直線
為參數),判斷直線![]() 與曲線
與曲線![]() 的位置關系.
的位置關系.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的各項均為正數,Sn是數列{an}的前n項和,且4Sn=an2+2an﹣3.
(1)求數列{an}的通項公式;
(2)已知bn=2n,求Tn=a1b1+a2b2+…+anbn的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com