若
=(1,2),
=(3,-4),則
在
方向上的投影為
.
考點:平面向量數(shù)量積的含義與物理意義
專題:平面向量及應(yīng)用
分析:投影即為|
|cosθ,利用數(shù)量積運算求出cosθ即可.
解答:解:設(shè)
,的夾角為θ
∵
=(1,2),=(3,-4)∴
||=,|
|=5,
•=-5
∴cosθ=
=-
故投影為|
|cosθ=-1
故答案為:-1
點評:本題主要考察了向量的數(shù)量積運算,難度不大,屬于基礎(chǔ)題.
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:
題型:
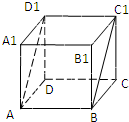
如圖,正方體ABCD-A
1B
1C
1D
1的棱長為1,則點A
1到平面ABC
1D
1的距離為( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
下面幾組對象可以構(gòu)成集合的是( )
| A、視力較差的同學(xué) |
| B、2013年的中國富豪 |
| C、充分接近2的實數(shù)的全體 |
| D、大于-2小于2的所有非負奇數(shù) |
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
已知隨機變量X服從正態(tài)分布N(3,1),且P(l≤X≤5)=0.6826,則P(X>5)=( )
| A、0.1588 |
| B、0.1587 |
| C、0.1586 |
| D、0.1585 |
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
在正六邊形ABCDEF中,若
=(1,-
),則
的坐標可能為( )
| A、(-1,) |
| B、(1,) |
| C、(,-1) |
| D、(,1) |
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
已知在平行四邊形ABCD中,AD=2AB,∠BAD=120°,P是面ABCD中一點,
=x
+y
,當點P在以A為圓心,|
|為半徑的圓上時,圓的方程( )
| A、x2+4y2+2xy=3 |
| B、x2+4y2-2xy=3 |
| C、4x2+y2+2xy=3 |
| D、4x2+y2-2xy=3 |
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
圓x2+y2-2x+6y+2=0的圓心坐標與半徑分別是( )
| A、(-1,3),r=2 |
| B、(1,-3),r=2 |
| C、(1,-3),r=4 |
| D、(1,-3),r=4 |
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
在等腰梯形ABCD中,E,F(xiàn)分別是底邊AB,CD的中點,把四邊形AEFD沿直線EF折起后所在的平面記為α,P∈α,設(shè)PB,PC與α所成的角分別為θ1,θ2(θ1,θ2均不等于零).若θ1=θ2,則點P的軌跡為( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
△ABC中,D是BC的中點,AD=m,BC=n,則
•
等于( )
| A、m2-n2 |
| B、m2+n2 |
| C、m2+n2 |
| D、m2-n2 |
查看答案和解析>>

 走進文言文系列答案
走進文言文系列答案