
分析 (1)先利用輔助角公式或二倍角的基本公式將函數化為y=Asin(ωx+φ)的形式,再利用周期公式求函數的最小正周期,最后將內層函數看作整體,放到正弦函數的增區間上,解不等式得函數的單調遞增區間;
(2)根據p是q的充分條件,即p⇒q,x∈[$\frac{π}{4}$,$\frac{π}{2}$],:|f(x)-m|<3恒成立,可得m的范圍.
解答 解:函數f(x)=2sin2($\frac{π}{4}$+x)-$\sqrt{3}$cos2x-1,x∈R.
化簡得f(x)=$1-cos(\frac{π}{2}+2x)$-$\sqrt{3}cos2x-1$=$sin2x-\sqrt{3}cos2x$=2sin(2x-$\frac{π}{3}$).
(1)f(x)的最小正周期T=$\frac{2π}{ω}=\frac{2π}{2}$=π,
令2kπ-$\frac{π}{2}$≤2x-$\frac{π}{3}$≤2kπ+$\frac{π}{2}$,解得:kπ-$\frac{π}{12}$≤x≤kπ+$\frac{5}{12}$π,(k∈Z);
∴f(x)的單調遞增區間為[kπ-$\frac{π}{12}$,kπ+$\frac{5}{12}$π](k∈Z);
(2)由p是q的充分條件,即p⇒q,
當x∈[$\frac{π}{4}$,$\frac{π}{2}$],
2x$-\frac{π}{3}$∈[$\frac{π}{6}$,$\frac{2π}{3}$],
∴1≤f(x)≤2,
∵|f(x)-m|<3,
∴-3<f(x)-m<3,
即-3+m<f(x)<3+m,
∴有$\left\{\begin{array}{l}{-3+m<1}\\{3+m>2}\end{array}\right.$,
解得:-1<m<4
∴m的取值范圍為(-1,4).
點評 本題主要考查對三角函數的化簡能力和三角函數的圖象和性質的運用,利用三角函數公式將函數進行化簡是解決本題的關鍵.屬于中檔題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | 6 | C. | 8 | D. | 14 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 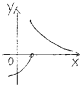 | B. | 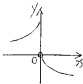 | C. | 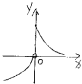 | D. | 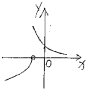 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com