
【題目】已知函數![]() ,
,![]() 為
為![]() 的導函數.
的導函數.
(1)求函數![]() 的單調區間;
的單調區間;
(2)若函數![]() 在
在![]() 上存在最大值0,求函數
上存在最大值0,求函數![]() 在
在![]() 上的最大值;
上的最大值;
(3)求證:當![]() 時,
時,![]() .
.
【答案】(1)見解析(2)![]() (3)見解析
(3)見解析
【解析】分析:(1)對a分類討論,求函數![]() 的單調區間.(2)根據函數
的單調區間.(2)根據函數![]() 在
在![]() 上存在最大值0轉化得到a=1,再求函數
上存在最大值0轉化得到a=1,再求函數![]() 在
在![]() 上的最大值.(3)先利用第2問轉化得到
上的最大值.(3)先利用第2問轉化得到![]() ,再證明
,再證明![]() ≤0.
≤0.
詳解:(1)由題意可知,![]()
![]() ,則
,則![]() ,
,
當![]() 時,
時,![]() ,∴
,∴![]() 在
在![]() 上單調遞增;
上單調遞增;
當![]() 時,解得
時,解得![]() 時,
時,![]() ,
,![]() 時,
時,![]()
∴![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減
上單調遞減
綜上,當![]() 時,
時,![]() 的單調遞增區間為
的單調遞增區間為![]() ,無遞減區間;當
,無遞減區間;當![]() 時,
時,![]() 的單調遞增區間為
的單調遞增區間為![]() ,單調遞減區間為
,單調遞減區間為![]() .
.
(2)由(1)可知,![]() 且
且![]() 在
在![]() 處取得最大值,
處取得最大值,
![]() ,即
,即![]() ,
,
觀察可得當![]() 時,方程成立
時,方程成立
令![]() ,
,![]()
當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]()
∴![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 單調遞增,
單調遞增,
∴![]() ,
,
∴當且僅當![]() 時,
時,![]() ,
,
所以![]() ,由題意可知
,由題意可知![]() ,
,![]() 在
在![]() 上單調遞減,
上單調遞減,
所以![]() 在
在![]() 處取得最大值
處取得最大值![]()
(3)由(2)可知,若![]() ,當
,當![]() 時,
時,![]() ,即
,即![]() ,
,
可得![]() ,
,
![]()
令![]() ,即證
,即證![]()
令![]() ,
,![]()
∵![]()
∴![]() ,又
,又![]() ,∴
,∴![]()
∴![]() ,
,![]() 在
在![]() 上單調遞減,
上單調遞減,![]() ,
,
∴![]() ,當且僅當
,當且僅當![]() 時等號成立
時等號成立
所以![]() .
.


科目:高中數學 來源: 題型:
【題目】為增進市民的環保意識,某市有關部門面向全體市民進行了一次環保知識的微信問卷測試活動,每位市民僅有一次參與問卷測試機會.通過抽樣,得到參與問卷測試的1000人的得分數據,制成頻率分布直方圖如圖所示.

(1)估計成績得分落在[86,100]中的概率.
(2)設這1000人得分的樣本平均值為![]() .
.
(i)求![]() (同一組數據用該區間的中點值作代表);
(同一組數據用該區間的中點值作代表);
(ii)有關部門為參與此次活動的市民贈送20元或10元的隨機話費,每次獲贈20元或10元的隨機話費的概率分別為![]() 和
和![]() .得分不低于
.得分不低于![]() 的可獲贈2次隨機話費,得分低于
的可獲贈2次隨機話費,得分低于![]() 的可獲贈1次隨機話費.求一位市民參與這次活動獲贈話費
的可獲贈1次隨機話費.求一位市民參與這次活動獲贈話費![]() 的平均估計值.
的平均估計值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() 中,底面 ABCD為矩形,側面為正三角形,且平面
中,底面 ABCD為矩形,側面為正三角形,且平面![]() 平面
平面 ![]() E 為 PD 中點,AD=2.
E 為 PD 中點,AD=2.
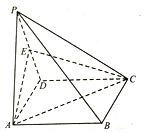
(1)證明平面AEC丄平面PCD;
(2)若二面角![]() 的平面角
的平面角![]() 滿足
滿足![]() ,求四棱錐
,求四棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了了解甲、乙兩校學生自主招生通過情況,從甲校抽取60人,從乙校抽取50人進行分析。

(1)根據題目條件完成上面2×2列聯表,并據此判斷是否有99%的把握認為自主招生通過情況與學生所在學校有關;
(2)現已知甲校![]() 三人在某大學自主招生中通過的概率分別為
三人在某大學自主招生中通過的概率分別為![]() ,
,![]() ,
,![]() ,用隨機變量X表示
,用隨機變量X表示![]() 三人在該大學自主招生中通過的人數,求X的分布列及期望
三人在該大學自主招生中通過的人數,求X的分布列及期望![]() .
.
參考公式:![]() .
.
參考數據:
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐P-ABCD中,底面ABCD為矩形,PD⊥平面ABCD,點E、F分別是AB和PC的中點.
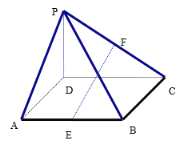
(1)求證:AB⊥平面PAD;
(2)求證:EF//平面PAD.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校為了加強學生數學核心素養的培養,鍛煉學生自主探究學習的能力,他們以教材第82頁第8題的函數![]() 為基本素材,研究該函數的相關性質,取得部分研究成果如下:
為基本素材,研究該函數的相關性質,取得部分研究成果如下:
①同學甲發現:函數![]() 的定義域為
的定義域為![]() ;
;
②同學乙發現:函數![]() 是偶函數;
是偶函數;
③同學丙發現:對于任意的![]() 都有
都有![]() ;
;
④同學丁發現:對于任意的![]() ,都有
,都有![]() ;
;
⑤同學戊發現:對于函數![]() 定義域中任意的兩個不同實數
定義域中任意的兩個不同實數![]() ,總滿足
,總滿足![]() .
.
其中所有正確研究成果的序號是__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年8月18日,舉世矚目的第18屆亞運會在印尼首都雅加達舉行,為了豐富亞運會志愿者的業余生活,同時鼓勵更多的有志青年加入志愿者行列,大會主辦方決定對150名志愿者組織一次有關體育運動的知識競賽(滿分120分)并計劃對成績前15名的志愿者進行獎勵,現將所有志愿者的競賽成績制成頻率分布直方圖,如圖所示,若第三組與第五組的頻數之和是第二組的頻數的3倍,試回答以下問題:
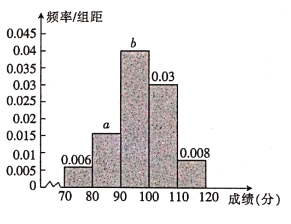
(1)求圖中![]() 的值;
的值;
(2)求志愿者知識競賽的平均成績;
(3)從受獎勵的15人中按成績利用分層抽樣抽取5人,再從抽取的5人中,隨機抽取2人在主會場服務,求抽取的這2人中其中一人成績在![]() 分的概率.
分的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線的中心在原點,焦點F1,F2在坐標軸上,離心率為![]() ,且過點
,且過點![]() .點M(3,m)在雙曲線上.
.點M(3,m)在雙曲線上.
(1)求雙曲線的方程;
(2)求證:![]() ;
;
(3)求△F1MF2的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com