
【題目】某學校為了加強學生數學核心素養的培養,鍛煉學生自主探究學習的能力,他們以教材第82頁第8題的函數![]() 為基本素材,研究該函數的相關性質,取得部分研究成果如下:
為基本素材,研究該函數的相關性質,取得部分研究成果如下:
①同學甲發現:函數![]() 的定義域為
的定義域為![]() ;
;
②同學乙發現:函數![]() 是偶函數;
是偶函數;
③同學丙發現:對于任意的![]() 都有
都有![]() ;
;
④同學丁發現:對于任意的![]() ,都有
,都有![]() ;
;
⑤同學戊發現:對于函數![]() 定義域中任意的兩個不同實數
定義域中任意的兩個不同實數![]() ,總滿足
,總滿足![]() .
.
其中所有正確研究成果的序號是__________.
【答案】①③④
【解析】①![]() ,故①正確;②
,故①正確;② ![]() ,奇函數,故②錯誤;③對于任意的
,奇函數,故②錯誤;③對于任意的![]() ,
, 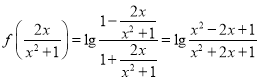
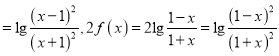 ,故③正確;④對于任意的
,故③正確;④對于任意的![]() ,有
,有![]() ,而
,而
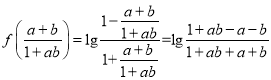 ,故④正確;⑤對于函數
,故④正確;⑤對于函數![]() 定義域
定義域
中任意的兩個不同實數![]() ,總滿足
,總滿足![]() ,即說明
,即說明![]() 是
是
增函數,但![]() 是減函數,故⑤錯誤,綜上①③④
是減函數,故⑤錯誤,綜上①③④
正確,故答案為①③④.
【 方法點睛】本題主要通過對多個命題真假的判斷,主要綜合考查函數的定義域、單調性、函數的奇偶性以及對數式的運算,屬于難題.這種題型綜合性較強,也是高考的命題熱點,同學們往往因為某一處知識點掌握不好而導致“全盤皆輸”,因此做這類題目更要細心、多讀題,盡量挖掘出題目中的隱含條件,另外,要注意從簡單的自己已經掌握的知識點入手,然后集中精力突破較難的命題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】如圖,正方體![]() 的棱長為4,動點E,F在棱
的棱長為4,動點E,F在棱![]() 上,動點P,Q分別在棱AD,CD上。若
上,動點P,Q分別在棱AD,CD上。若![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() 大于零),則四面體PEFQ的體積
大于零),則四面體PEFQ的體積
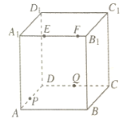
A.與![]() 都有關B.與m有關,與
都有關B.與m有關,與![]() 無關
無關
C.與p有關,與![]() 無關D.與π有關,與
無關D.與π有關,與![]() 無關
無關
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,點
中,點![]() ,直線
,直線![]() ,圓
,圓![]() .
.
(1)求![]() 的取值范圍,并求出圓心坐標;
的取值范圍,并求出圓心坐標;
(2)有一動圓![]() 的半徑為
的半徑為![]() ,圓心在
,圓心在![]() 上,若動圓
上,若動圓![]() 上存在點
上存在點![]() ,使
,使![]() ,求圓心
,求圓心![]() 的橫坐標
的橫坐標![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某機構為了解某地區中學生在校月消費情況,隨機抽取了 100名中學生進行調查.如圖是根據調査的結果繪制的學生在校月消費金額的頻率分布直方圖.已知![]() 三個金額段的學生人數成等差數列,將月消費金額不低于550元的學生稱為“高消費群”.
三個金額段的學生人數成等差數列,將月消費金額不低于550元的學生稱為“高消費群”.
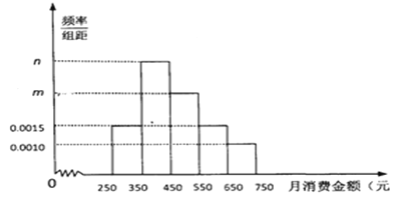
(1)求![]() 的值,并求這100名學生月消費金額的樣本平均數
的值,并求這100名學生月消費金額的樣本平均數![]() (同一組中的數據用該組區間的中點值作代表);
(同一組中的數據用該組區間的中點值作代表);
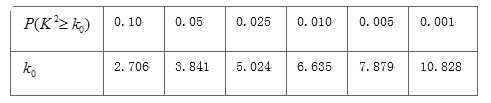
(2)根據已知條件完成下面![]() 列聯表,并判斷能否有
列聯表,并判斷能否有![]() 的把握認為“高消費群”與性別有關?
的把握認為“高消費群”與性別有關?

附: ![]() (其中
(其中![]() 樣本容量)
樣本容量)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的前n項和為Sn,滿足Sn=2an-1(n∈N*),數列{bn}滿足nbn+1-(n+1)bn=n(n+1)(n∈N*),且b1=1.
(1)證明數列{![]() }為等差數列,并求數列{an}和{bn}的通項公式;
}為等差數列,并求數列{an}和{bn}的通項公式;
(2)若cn=(-1)n-1![]() ,求數列{cn}的前n項和T2n;
,求數列{cn}的前n項和T2n;
(3)若dn=an![]() ,數列{dn}的前n項和為Dn,對任意的n∈N*,都有Dn≤nSn-a,求實數a的取值范圍.
,數列{dn}的前n項和為Dn,對任意的n∈N*,都有Dn≤nSn-a,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在正方體![]() 中,點
中,點![]() ,
,![]() 分別為棱
分別為棱![]() ,
,![]() 的中點,點
的中點,點![]() 為上底面的中心,過
為上底面的中心,過![]() ,
,![]() ,
,![]() 三點的平面把正方體分為兩部分,其中含
三點的平面把正方體分為兩部分,其中含![]() 的部分為
的部分為![]() ,不含
,不含![]() 的部分為
的部分為![]() ,連結
,連結![]() 和
和![]() 的任一點
的任一點![]() ,設
,設![]() 與平面
與平面![]() 所成角為
所成角為![]() ,則
,則![]() 的最大值為
的最大值為

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某興趣小組欲研究晝夜溫差大小與患感冒人數多少之間的關系,他們分別到氣象局與某醫院抄錄了1至6月份每月10號的晝夜溫差情況與因患感冒而就診的人數,得到如下資料:

該興趣小組確定的研究方案是:先用2、3、4、5月的4組數據求線性回歸方程,再用1月和6月的2組數據進行檢驗.
(1)請根據2、3、4、5月的數據,求出y關于x的線性回歸方程![]() ;
;
(2)若由線性回歸方程得到的估計數據與所選出的檢驗數據的誤差均不超過2人,則認為得到的線性回歸方程是理想的,試問該小組所得線性回歸方程是否理想?
(參考公式:  ,
,![]()
 )
)
參考數據:11×25+13×29+12×26+8×16=![]() 1092,112+132+122+82=498.
1092,112+132+122+82=498.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com