
分析 (1)由周期求得ω,由函數g(x)為奇函數求得φ和b的值,從而得到函數f(x)的解析式.
(2)令 2kπ-$\frac{π}{2}$≤2x+$\frac{π}{3}$≤2kπ+$\frac{π}{2}$,k∈z,求得x的范圍,即可得到函數的增區間.同理,令2kπ+$\frac{π}{2}$≤2x+$\frac{π}{3}$≤2kπ+$\frac{3π}{2}$,k∈z,求得x的范圍,即可得到函數的減區間.
解答 解:(1)∵$\frac{2π}{ω}$=2×$\frac{π}{2}$,∴ω=2,∴f(x)=sin(2x+φ)-b.
又g(x)=sin[2(x-$\frac{π}{6}$)+φ]-b+$\sqrt{3}$為奇函數,且0<φ<π,則φ=$\frac{π}{3}$,b=$\sqrt{3}$,
故f(x)=sin(2x+$\frac{π}{3}$)-$\sqrt{3}$.
(2)令 2kπ-$\frac{π}{2}$≤2x+$\frac{π}{3}$≤2kπ+$\frac{π}{2}$,k∈z,求得-$\frac{5π}{12}$+kπ≤x≤$\frac{π}{12}$+kπ,(k∈Z),
故函數的增區間為[-$\frac{5π}{12}$+kπ,$\frac{π}{12}$+kπ](k∈Z).
令2kπ+$\frac{π}{2}$≤2x+$\frac{π}{3}$≤2kπ+$\frac{3π}{2}$,k∈z,求得 $\frac{π}{12}$+kπ≤x≤$\frac{7π}{12}$+kπ,(k∈Z),
故函數的減區間為[$\frac{π}{12}$+kπ,$\frac{7π}{12}$+kπ](k∈Z).
點評 本題主要考查由函數y=Asin(ωx+∅)的部分圖象求解析式,正弦函數的單調性,不等式的性質應用,函數的奇偶性,函數的恒成立問題,屬于中檔題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 姓名 | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 |
| 貝航 | 9 | 9 | 10 | 8 | 9 | 9 | 6 | 9 | 9 | 7 |
| 姓名 | 貝航 | 黃韋嘉 | 李萱 | 劉紫璇 | 羅迪威 | 王安國 | 肖悅 | 楊清源 | 袁佳儀 | 周紫薇 |
| 性別 | 女 | 男 | 女 | 女 | 男 | 男 | 女 | 男 | 女 | 女 |
| 最終得分 | a | 9.22 | 8.50 | 8.81 | 8.43 | 8.91 | 8.12 | 7.95 | 9.31 | 7.79 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
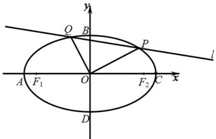 如圖,在直角坐標系xOy中,橢圓$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左右焦點分別為F1,F2,左、右、上、下四個頂點分別為A,C,B,D,四邊形F1BF2D的面積與四邊形ABCD的面積的比值為$\frac{{\sqrt{6}}}{3}$.
如圖,在直角坐標系xOy中,橢圓$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左右焦點分別為F1,F2,左、右、上、下四個頂點分別為A,C,B,D,四邊形F1BF2D的面積與四邊形ABCD的面積的比值為$\frac{{\sqrt{6}}}{3}$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com