
分析 (1)將不等式a2+b2≥2ab,a2+c2≥2ac,b2+c2≥2bc相加得出a2+b2+c2≥ab+ac+bc,再將a+b+c=1兩邊平方即可得出結(jié)論;
(2)$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}$=(a+b+c)($\frac{1}{a}+\frac{1}{b}+\frac{1}{c}$),在利用基本不等式即可得出結(jié)論.
解答 證明:(1)∵a,b,c均為正數(shù),
∴a2+b2≥2ab,a2+c2≥2ac,b2+c2≥2bc,
以上三式相加得:2(a2+b2+c2)≥2(ab+ac+bc),
∴a2+b2+c2≥ab+ac+bc;
∴(a+b+c)2=a2+b2+c2+2(ab+ac+bc)≥3(ab+bc+ac),
∵a+b+c=1,
∴1≥3(ab+bc+ac)
∴ab+bc+ca≤$\frac{1}{3}$(當(dāng)且僅當(dāng)a=b=c=$\frac{1}{3}$時(shí)取“=”).
(2)∵a,b,c均為正數(shù),且a+b+c=1,
∴a+b+c≥3$\root{3}{abc}$,$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}$≥3$\root{3}{\frac{1}{abc}}$,
∴$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}$=(a+b+c)($\frac{1}{a}+\frac{1}{b}+\frac{1}{c}$)≥3$\root{3}{abc}$•3$\root{3}{\frac{1}{abc}}$=9.
當(dāng)且僅當(dāng)a=b=c=$\frac{1}{3}$時(shí)取“=”.
點(diǎn)評(píng) 本題考查了不等式的證明,基本不等式的應(yīng)用,屬于中檔題.


 新課標(biāo)階梯閱讀訓(xùn)練系列答案
新課標(biāo)階梯閱讀訓(xùn)練系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
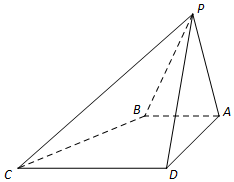 如圖四棱錐P-ABCD中,側(cè)面PAD⊥底面ABCD.△PAD是正三角形,四邊形ABCD是直角梯形,AB∥CD,AD=CD=2AB,點(diǎn)E為PD中點(diǎn).
如圖四棱錐P-ABCD中,側(cè)面PAD⊥底面ABCD.△PAD是正三角形,四邊形ABCD是直角梯形,AB∥CD,AD=CD=2AB,點(diǎn)E為PD中點(diǎn).查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com