
【題目】(1)如果把棱柱中過不相鄰的兩條側棱的截面叫棱柱的“對角面”,則平行六面體的對角面的形狀是_______,直平行六面體的對角面的形狀是______;
(2)過正三棱柱底面的一邊和兩底面中心連線段的中點作截面,則這個截面的形狀為_____.
【答案】平行四邊形 矩形 梯形
【解析】
(1)根據棱柱的定義,側棱平行且相等,直六面體側棱與底面垂直,即可得出結論;
(2)將過正三棱柱底面的一邊和兩底面中心連線段的中點的截面延展,利用輔助平面做相交線和平行線,確定出與底面和側面的交線,即可得出截面形狀.
(1)由棱柱的定義可得,側棱平行且相等,
過不相鄰的兩條側棱的截面對邊平行且相等的四邊形,
所以“對角面”是平行四邊形;
直平行六面體的側棱與底面垂直,所以側棱垂直底面的對角線,
所以“對角面”是矩形;
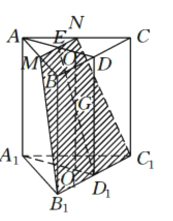
(2)如圖正三棱柱![]() ,上下底面的中心為
,上下底面的中心為![]() ,
,
延長![]() ,分別與
,分別與![]() 交于
交于![]() ,連
,連![]() ,
,
則![]() 在同一個平面內,在平面
在同一個平面內,在平面![]() 中,
中,
過![]() 及
及![]() 中點
中點![]() 作直線與
作直線與![]() 相交于
相交于![]() ,
,
過![]() 作
作![]() 的平行線分別與
的平行線分別與![]() 交于
交于![]() ,
,![]()
則梯形![]() 為過點
為過點![]() 和點
和點![]() 的截面.
的截面.
故答案為: (1)平行四邊形,矩形;(2) 梯形.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】設n為給定的大于2的整數。有n個外表上沒有區別的袋子,第k(k=1,2,···,n)個袋中有k個紅球,n-k個白球。將這些袋子混合后,任選一個袋子,并且從中連續取出三個球(每次取出不放回)。求第三次取出的為白球的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠的檢驗員為了檢測生產線上生產零件的情況,從產品中隨機抽取了![]() 個進行測量,根據所測量的數據畫出頻率分布直方圖如下:
個進行測量,根據所測量的數據畫出頻率分布直方圖如下:
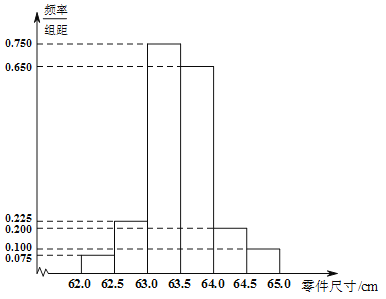
注:尺寸數據在![]() 內的零件為合格品,頻率作為概率.
內的零件為合格品,頻率作為概率.
(Ⅰ) 從產品中隨機抽取![]() 件,合格品的個數為
件,合格品的個數為![]() ,求
,求![]() 的分布列與期望;
的分布列與期望;
(Ⅱ) 從產品中隨機抽取![]() 件,全是合格品的概率不小于
件,全是合格品的概率不小于![]() ,求
,求![]() 的最大值;
的最大值;
(Ⅲ) 為了提高產品合格率,現提出![]() 兩種不同的改進方案進行試驗.若按
兩種不同的改進方案進行試驗.若按![]() 方案進行試驗后,隨機抽取
方案進行試驗后,隨機抽取![]() 件產品,不合格個數的期望是
件產品,不合格個數的期望是![]() ;若按
;若按![]() 方案試驗后,抽取
方案試驗后,抽取![]() 件產品,不合格個數的期望是
件產品,不合格個數的期望是![]() ,你會選擇哪個改進方案?
,你會選擇哪個改進方案?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】假設要考察某公司生產的![]() 克袋裝牛奶的質量是否達標,現從
克袋裝牛奶的質量是否達標,現從![]() 袋牛奶中抽取
袋牛奶中抽取![]() 袋牛奶進行檢驗,利用隨機數表抽樣時,先將
袋牛奶進行檢驗,利用隨機數表抽樣時,先將![]() 袋牛奶按
袋牛奶按![]() 、
、![]() 、
、![]() 、
、![]() 進行編號,如果從隨機數表第
進行編號,如果從隨機數表第![]() 行第
行第![]() 列開始向右讀,請你依次寫出最先檢測的
列開始向右讀,請你依次寫出最先檢測的![]() 袋牛奶的編號_____________,_____________,_____________,_____________,_____________.(下面摘取了隨機數表第
袋牛奶的編號_____________,_____________,_____________,_____________,_____________.(下面摘取了隨機數表第![]() 行至第
行至第![]() 行)
行)
8842 1753 3157 2455 0688 7704 7476 7217 6335 0258 3921 2067 64
6301 6378 5916 9556 6719 9810 5071 7512 8673 5807 4439 5238 79
3321 1234 2978 6456 0782 5242 0744 3815 5100 1342 9966 0279 54
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系,已知曲線
軸的正半軸為極軸建立極坐標系,已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,過點
,過點![]() 的直線
的直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),直線
為參數),直線![]() 與曲線
與曲線![]() 相交于
相交于![]() ,
,![]() 兩點.
兩點.
(1)寫出曲線![]() 的直角坐標方程和直線
的直角坐標方程和直線![]() 的普通方程;
的普通方程;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,長方體![]() 的長,寬,高分別為4,3,5,現有一甲殼蟲從
的長,寬,高分別為4,3,5,現有一甲殼蟲從![]() 點出發沿長方體表面爬行到
點出發沿長方體表面爬行到![]() 點來獲取食物.
點來獲取食物.
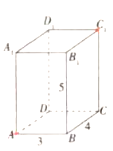
(1)甲殼蟲想盡快獲取食物可通過哪些路徑獲取?
(2)哪條獲取食物的路徑最短?最短為多少?
(3)此類問題的一般處理方法是什么?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】電視傳媒為了解某市100萬觀眾對足球節目的收視情況,隨機抽取了100名觀眾進行調查.如圖是根據調查結果繪制的觀眾每周平均收看足球節目時間的頻率分布直方圖,將每周平均收看足球節目時間不低于1.5小時的觀眾稱為“足球迷”, 并將其中每周平均收看足球節目時間不低于2.5小時的觀眾稱為“鐵桿足球迷”.
(1)試估算該市“足球迷”的人數,并指出其中“鐵桿足球迷”約為多少人;
(2)該市要舉辦一場足球比賽,已知該市的足球場可容納10萬名觀眾.根據調查,如果票價定為100元/張,則非“足球迷”均不會到現場觀看,而“足球迷”均愿意前往現場觀看.如果票價提高![]() 元/張
元/張![]() ,則“足球迷”中非“鐵桿足球迷”愿意前往觀看的人數會減少
,則“足球迷”中非“鐵桿足球迷”愿意前往觀看的人數會減少![]() ,“鐵桿足球迷”愿意前往觀看的人數會減少
,“鐵桿足球迷”愿意前往觀看的人數會減少![]() .問票價至少定為多少元/張時,才能使前往現場觀看足球比賽的人數不超過10萬人?
.問票價至少定為多少元/張時,才能使前往現場觀看足球比賽的人數不超過10萬人?

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了迎接旅游旺季的到來,少林寺設置了一個專門安排旅客住宿的客棧,寺廟的工作人員發現為游客準備的食物有些月份剩余不少,浪費很嚴重,為了控制經營成本,減少浪費,就想適時調整投入.為此他們統計每個月入住的游客人數,發現每年各個月份來客棧入住的游客人數會呈現周期性的變化,并且有以下規律:
①每年相同的月份,入住客棧的游客人數基本相同;
②入住客棧的游客人數在![]() 月份最少,在
月份最少,在![]() 月份最多,相差約
月份最多,相差約![]() 人;
人;
③![]() 月份入住客棧的游客約為
月份入住客棧的游客約為![]() 人,隨后逐月增加直到
人,隨后逐月增加直到![]() 月份達到最多.
月份達到最多.
(1)試用一個正弦型三角函數描述一年中入住客棧的游客人數與月份之間的關系;
(2)請問哪幾個月份要準備![]() 份以上的食物?
份以上的食物?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com