【題目】設n為給定的大于2的整數。有n個外表上沒有區別的袋子，第k(k=1,2,···,n)個袋中有k個紅球，n-k個白球。將這些袋子混合后，任選一個袋子，并且從中連續取出三個球(每次取出不放回)。求第三次取出的為白球的概率。
【答案】
【解析】
設選出的是第k個袋子，連續三次取球的方法數為n(n-1)(n-2).
第三次取出的是白球的三次取球顏色有如下四種情形:
(白，白，白)取法數為 (n-k)(n-k-1)(n-k-2)，
(白，紅，白)取法數為k(n-k)(n-k-1)，
(紅，白，白)取法數為k(n-k)(n-k-1)，
(紅，紅,白)取法數為k(k-1)(n-k).
從而，第三次取出的是白球的種數為
（n-k）（n-k-1）（n-k-2）+k（n-k）（n-k-1）+k（n-k）（n-k-1）+k（k-1）（n-k）
=（n-1）（n-2）（n-k）.
則在第h個袋子中第三次取出的是白球的概率為
而選到第k個袋子的概率為
，故所求的概率為
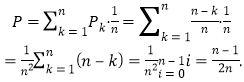
孟建平名校考卷系列答案科目：高中數學 來源： 題型：
【題目】如圖，已知
垂直于梯形
所在的平面，
，
為
的中點，
，
.若四邊形
為矩形，線段
與
交于點
.
（1）證明：
∥平面
.
（2）求二面角
的大小。
（3）在線段
上是否存在一點
，使得
與平面
所成角的大小為
？若存在，請求出
的長；若不存在，請說明理由。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，點
，直線
的參數方程為
（
為參數），以
為極點，
軸的非負半軸為極軸建立極坐標系，曲線
的極坐標方程為
．
當
時，判斷直線與曲線的位置關系；
若直線與曲線相切于點
，求
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
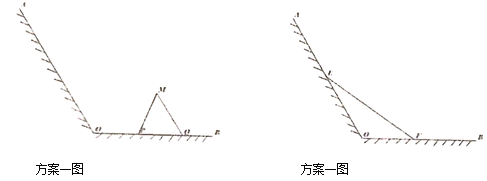
【題目】江心洲有一塊如圖所示的江邊，
，
為岸邊，岸邊形成
角，現擬在此江邊用圍網建一個江水養殖場，有兩個方案：方案l：在岸邊上取兩點
，用長度為
的圍網依托岸邊線
圍成三角形
（
，
兩邊為圍網）；方案2：在岸邊，上分別取點
，用長度為的圍網
依托岸邊圍成三角形
.請分別計算
，
面積的最大值，并比較哪個方案好.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】將
方格紙中每個小方格染三種顏色之一，使得每種顏色的小方格的個數相等．若相鄰兩個小方格的顏色不同，稱他們的公共邊為“分割邊”，則分割邊條數的最小值為（ ）
A.33B.56C.64D.78
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的左、右焦點分別為F1，F2，離心率
，且橢圓的短軸長為2．
（1）求橢圓的標準方程；
（2）已知直線l1，l2過右焦點F2，且它們的斜率乘積為﹣1，設l1，l2分別與橢圓交于點A，B和C，D．①求AB＋CD的值；②設AB的中點M，CD的中點為N，求△OMN面積的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某次考試中500名學生的物理（滿分為150分）成績服從正態分布
，數學成績的頻率分布直方圖如圖所示．
（Ⅰ）如果成績大于135分為特別優秀，那么本次考試中的物理、數學特別優秀的大約各有多少人？
（Ⅱ）如果物理和數學兩科都特別優秀的共有4人，是否有99.9%的把握認為物理特別優秀的學生，數學也特別優秀？
附：①若
，則
②表及公式：
| 0.50 | 0.40 | … | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | … | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（1）如果把棱柱中過不相鄰的兩條側棱的截面叫棱柱的“對角面”，則平行六面體的對角面的形狀是_______，直平行六面體的對角面的形狀是______；
（2）過正三棱柱底面的一邊和兩底面中心連線段的中點作截面，則這個截面的形狀為_____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
