【題目】四棱錐
中，底面
為直角梯形，
，
，
，
平面，
，
為
中點.
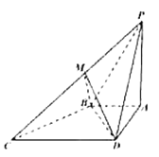
（Ⅰ）求證：平面
平面
；
（Ⅱ）求二面角
的余弦值.
【答案】(1)見證明；(2) 
【解析】
（1）在
中，由余弦定理，
，又
，
，得到
，
，
由線面垂直的判定定理，得
平面
，進而利用面面垂直的判定定理，證得平面
平面
.
（2）以
為原點，
，
，
為
，
，
軸，建立空間直角坐標系，求得平面
的法向量為
和平面平面的一個法向量為
，利用向量的夾角公式，即可求解.
（1）在直角梯形中，
，
，
在中，由余弦定理，，又，，
有
，
是等腰三角形，所以，，
由線面垂直的判定定理，得平面，
又由面面垂直的判定定理，即可得到平面平面.
（2）以為原點，，，為，，軸，建立空間直角坐標系，
則
，
，
，
，
，
有
，，
，
令平面的法向量為
，由
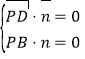，可得一個，
由（1）可知平面的一個法向量為，
所以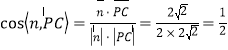
,
所以二面角
的余弦值為.
暑假作業海燕出版社系列答案科目：高中數學 來源： 題型：
【題目】
義烏國際馬拉松賽，某校要從甲乙丙丁等
人中挑選
人參加比賽，其中甲乙丙丁
人中至少有
人參加且甲乙不同時參加，丙丁也不同時參加，則不同的報名方案有（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
在極坐標系中，曲線
的極坐標方程為
，點
的極坐標為
，以極點
為極點，以
軸正半軸為極軸建立極坐標系.
（1）曲線的直角坐標方程和點的直角坐標；
（2）若過點且傾斜角為
的直線
，點
為曲線上任意一點，求點到直線的最小距離.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某研究機構隨機調查了
，
兩個企業各100名員工，得到了企業員工月均收入的頻數分布表以及企業員工月均收入的統計圖如下：
企業：
工資 | 人數 |
| 5 |
| 10 |
| 20 |
| 42 |
| 18 |
| 3 |
| 1 |
| 1 |
企業：
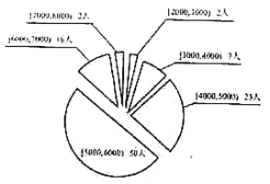
（1）若將頻率視為概率，現從企業中隨機抽取一名員工，求該員工月均收入不低于5000元的概率；
（2）（i）若從企業的月均收入在
員工中，按分層抽樣的方式抽取7人，而后在此7人中隨機抽取2人，則2人月均收入都不在
的概率是多少？
（ii）若你是一名即將就業的大學生，根據上述調查結果，并結合統計學相關知識，你會選擇去哪個企業就業，并說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，四邊形ABCD為矩形，沿AB將△ADC翻折成
.設二面角
的平面角為
，直線
與直線BC所成角為
，直線與平面ABC所成角為
，當為銳角時，有
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
的展開式中第5項與第7項的二項數系數相等，且展開式的各項系數之和為1024，則下列說法正確的是（ ）
A.展開式中奇數項的二項式系數和為256
B.展開式中第6項的系數最大
C.展開式中存在常數項
D.展開式中含
項的系數為45
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】我市南澳縣是廣東唯一的海島縣，海區面積廣闊，發展太平洋牡蠣養殖業具有得天獨厚的優勢，所產的“南澳牡蠣”是中國國家地理標志產品，產量高、肉質肥、營養好，素有“海洋牛奶精品”的美譽．根據養殖規模與以往的養殖經驗，產自某南澳牡蠣養殖基地的單個“南澳牡蠣”質量（克）在正常環境下服從正態分布
．
（1）購買10只該基地的“南澳牡蠣”，會買到質量小于20g的牡蠣的可能性有多大？
（2）2019年該基地考慮增加人工投入，現有以往的人工投入增量x（人）與年收益增量y（萬元）的數據如下：
人工投入增量x（人） | 2 | 3 | 4 | 6 | 8 | 10 | 13 |
年收益增量y（萬元） | 13 | 22 | 31 | 42 | 50 | 56 | 58 |
該基地為了預測人工投入增量為16人時的年收益增量，建立了y與x的兩個回歸模型：
模型①：由最小二乘公式可求得y與x的線性回歸方程：
；
模型②：由散點圖的樣本點分布，可以認為樣本點集中在曲線：
的附近，對人工投入增量x做變換，令
，則
，且有
．
（i）根據所給的統計量，求模型②中y關于x的回歸方程（精確到0.1）；
（ii）根據下列表格中的數據，比較兩種模型的相關指數
，并選擇擬合精度更高、更可靠的模型，預測人工投入增量為16人時的年收益增量．
回歸模型 | 模型① | 模型② |
回歸方程 |
|
|
| 182.4 | 79.2 |
附：若隨機變量
，則
，
；
樣本
的最小二乘估計公式為：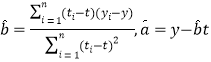
，
另，刻畫回歸效果的相關指數
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
