
分析 (Ⅰ)先求導數fˊ(x)然后在函數的定義域內解不等式fˊ(x)>0和fˊ(x)<0,fˊ(x)>0的區間為單調增區間,fˊ(x)<0的區間為單調減區間;
(Ⅱ)求出函數的導數,得到函數的單調區間,求出函數的最大值和最小值即可;
(Ⅲ)方程f(x)=x2-x-a變形為x-2lnx-a=0,令g(x)=x-2lnx-a(x>0),利用數形結合的思想,要求g(x)在區間[1,3]上恰好有兩個相異的零點.通過g(x)的單調性及最值,極值求解.
解答 解:(I)由函數f(x)=x2-2lnx知其定義域為{x|x>0},
∵f′(x)=2x-$\frac{2}{x}$=$\frac{2(x+1)(x-1)}{x}$,
令f'(x)>0,解得:x>1;令f'(x)<0,解得:0<x<1
∴函數f(x)單調增區間是(1,+∞);減區間是(0,1);
(II)由f′(x)=0,解得:x=1或-1(舍),
由(I)知f(x)在[$\frac{1}{e}$,1]上遞減,在[1,e]上遞增,
當x=1時,f(x)取最小值f(1)=1,
又f($\frac{1}{e}$)=$\frac{1}{{e}^{2}}$+2,f(e)=e2-2,且e2-2>$\frac{1}{{e}^{2}}$+2,
∴f(x)在[$\frac{1}{e}$,e]上的最小值為1,最大值為e2-2;
(III)方程f(x)=x2-x-a,即x-2lnx-a=0,記g(x)=x-2lnx-a,
∵g′(x)=$\frac{x-2}{x}$,
由g′(x)>0,得x>2或x<0(舍去),g′(x)<0得0<x<2,
∴g(x)在[1,2]上遞減,在[2,3]上遞增,
為使方程f(x)=x2-x-a在區間[1,3]上恰好有兩個相異的實根,
只需g(x)=0在[1,2]和[2,3]上各有一個實根,
于是$\left\{\begin{array}{l}{g(1)≥0}\\{g(2)<0}\\{g(3)≥0}\end{array}\right.$,即$\left\{\begin{array}{l}{1-a≥0}\\{2-2ln2-a<0}\\{3-2ln3-a≥0}\end{array}\right.$,
∴2-2ln2<a≤3-2ln3,
即實數a的取值范圍是(2-2ln2,3-2ln3].
點評 本題考查導數知識的綜合運用,考查函數的單調性,恒成立問題,函數與方程,數形結合思想,屬于中檔題.


 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案科目:高中數學 來源: 題型:選擇題
| A. | 若l∥α,m∥α,則l∥m | B. | 若l⊥m,m?α,則l⊥α | C. | 若l∥α,m?α,則l∥m | D. | 若l⊥α,l∥m,則m⊥α |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
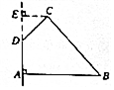 如圖,在四邊形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2$\sqrt{2}$,AD=2,則四邊形ABCD繞AD旋轉一周所成幾何體的表面積為( )
如圖,在四邊形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2$\sqrt{2}$,AD=2,則四邊形ABCD繞AD旋轉一周所成幾何體的表面積為( )| A. | (60+4$\sqrt{2}$)π | B. | (60+8$\sqrt{2}$)π | C. | (56+8$\sqrt{2}$)π | D. | (56+4$\sqrt{2}$)π |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
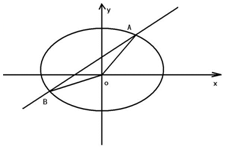 已知橢圓C的中心在坐標原點,一個焦點的坐標為$(\sqrt{3},0)$,橢圓C經過點P$(1,\frac{{\sqrt{3}}}{2})$.
已知橢圓C的中心在坐標原點,一個焦點的坐標為$(\sqrt{3},0)$,橢圓C經過點P$(1,\frac{{\sqrt{3}}}{2})$.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com