

分析 (1)先分別觀察給出正方體的個數為:1,1+4,1+4+8,…從而得出a5;
(2)將(1)總結一般性的規律:an+1與an的關系式,再從總結出來的一般性的規律轉化為特殊的數列再求解即得.
(3)利用裂項法求和,即可得出結論.
解答 解:(1)∵a1=1,a2=5,a3=13,a4=25,
∴a2-a1=4=4×1.
a3-a2=8=4×2,
a4-a3=12=4×3,
a5-a4=16=4×4
∴a5=25+4×4=41.
(2)由上式規律得出an+1-an=4n.
∴an-a1=4[1+2+…+(n-2)+(n-1)]=2(n-1)•n,
∴an=2n2-2n+1.…(12分)
(3)∵$\frac{1}{a_1}+\frac{1}{{{a_2}-1}}+…+\frac{1}{{{a_n}-1}}$=1+$\frac{1}{2}$(1-$\frac{1}{2}$+$\frac{1}{2}-\frac{1}{3}$+…+$\frac{1}{n-1}$-$\frac{1}{n}$)=$\frac{3}{2}-\frac{1}{2n}$.
點評 本題主要考查歸納推理,其基本思路是先分析具體,觀察,總結其內在聯系,得到一般性的結論,若求解的項數較少,可一直推理出結果,若項數較多,則要得到一般求解方法,再求具體問題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
| A. | [0,3] | B. | [1,3] | C. | [1,+∞) | D. | [3,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
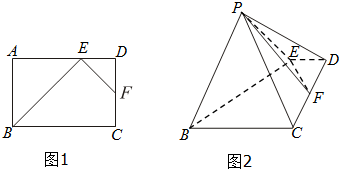 如圖1,在矩形ABCD中,點E為邊AD上靠近D的三等分點,點F為邊CD的中點,AB=AE=4,現將△ABE沿BE邊折至△PBE位置,且平面PBE⊥平面BCDE.
如圖1,在矩形ABCD中,點E為邊AD上靠近D的三等分點,點F為邊CD的中點,AB=AE=4,現將△ABE沿BE邊折至△PBE位置,且平面PBE⊥平面BCDE.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $(0,\frac{π}{4})$ | B. | $(\frac{π}{4},\frac{π}{2})$ | C. | $(0,\frac{π}{2})$ | D. | $(\frac{π}{2},π)$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 有最小值-3,最大值3 | B. | 有最小值-3,無最大值 | ||
| C. | 最小值-3,有最大值$\frac{3}{2}$ | D. | 無最小值,有最大值$\frac{3}{2}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com