
 如圖,在四棱錐P-ABCD中,PD⊥底面ABCD,底面ABCD是邊長為2的正方形,PD=DC,E,F分別是AB,PB的中點.
如圖,在四棱錐P-ABCD中,PD⊥底面ABCD,底面ABCD是邊長為2的正方形,PD=DC,E,F分別是AB,PB的中點.分析 (1)推導出AD⊥DC,PD⊥CD,從而CD⊥平面PAD,進而CD⊥PA,再由EF∥PA,能證明EF⊥CD.
(2)當G為AD的中點時,設BD的中點為O,連接OF,OG,PG,GB.推導出BC⊥平面GFO,從而GF⊥BC,推導出GF⊥PB,由此得到GF⊥平面PCB.
(3)三棱錐B-DEF的體積VB-DEF=VF-BDE.由此能求出結果.
解答 (本題滿分14分)
證明:(1)因為底面ABCD是的正方形,所以AD⊥DC.
又PD⊥底面ABCD,所以PD⊥CD.
又AD∩PD=D,所以CD⊥平面PAD,(2分)
又PA?平面PAD,所以CD⊥PA. (4分)
因為E,F分別是AB,PB的中點,所以EF∥PA,(5分)
所以EF⊥CD. (6分)
解:(2)當G為AD的中點時,FG⊥平面PCB.
證明:設BD的中點為O,連接OF,OG,PG,GB.
因為O,F,G分別是BD,PB,AD的中點,所以FO∥PD,GO∥AB.
因為AB⊥BC,所以GO⊥BC,所以BC⊥平面GFO. (8分)
又GF?平面GFO,所以GF⊥BC.
因為PD=DC=2,所以$PG=GB=\sqrt{5}$.
又F是PB的中點,所以GF⊥PB,
所以GF⊥平面PCB. (11分)
(3)∵PD⊥底面ABCD,O,F分別是DB,PB的中點,
∴FO⊥平面BDE,且FO=$\frac{1}{2}$PD=1,
S△BDE=$\frac{1}{2}×AD×BE=\frac{1}{2}×2×1$=1,
∴三棱錐B-DEF的體積${V_{B-DEF}}={V_{F-BDE}}=\frac{1}{3}{S_{△BDE}}•(\frac{1}{2}PD)=\frac{1}{3}$. (14分)
點評 本題考查線線垂直的證明,考查滿足條件的點的位置的確定,考查三棱錐的體積的求法,是中檔題,解題時要認真審題,注意空間思維能力的培養.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | y=1 | B. | y=$\frac{(\sqrt{x})^{2}}{x}$ | C. | y=$\frac{x}{x}$ | D. | y=$\frac{|x|+1}{|x|+1}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
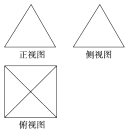 一個幾何體的三視圖如圖所示,正視圖和側視圖都是等邊三角形,且該幾何體的四個點在空間直角坐標系O-xyz中的坐標分別是(0,0,0),(2,0,0),(0,2,0),則第五個頂點的坐標可能為( )
一個幾何體的三視圖如圖所示,正視圖和側視圖都是等邊三角形,且該幾何體的四個點在空間直角坐標系O-xyz中的坐標分別是(0,0,0),(2,0,0),(0,2,0),則第五個頂點的坐標可能為( )| A. | (1,1,1) | B. | (1,1,$\sqrt{2}$) | C. | (1,1,$\sqrt{3}$) | D. | (2,2,$\sqrt{3}$) |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $4\sqrt{5}$ | B. | $\sqrt{3}$ | C. | $3\sqrt{3}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com