
分析 (I)利用“累加求和”與“裂項求和”方法即可得出.
(Ⅱ)當k≥2,有$a_k^2=\frac{1}{{{{(3k-2)}^2}}}<\frac{1}{(3k-4)(3k-1)}=\frac{1}{3}(\frac{1}{3k-4}-\frac{1}{3k-1})$,利用“裂項求和”方法與數列的單調性即可證明.
解答 (Ⅰ)解:由已知,對n≥2,$\frac{1}{{n{a_{n+1}}}}=\frac{1}{{(n-1){a_n}}}-\frac{1}{n(n-1)}$,
即 $\frac{1}{{n{a_{n+1}}}}-\frac{1}{{(n-1){a_n}}}=-(\frac{1}{n-1}-\frac{1}{n})$,
于是,$\sum_{k=2}^{n-1}{[{\frac{1}{{k{a_{k+1}}}}-\frac{1}{{(k-1){a_k}}}}]}=-\sum_{k=2}^{n-1}{({\frac{1}{k-1}-\frac{1}{k}})}=-(1-\frac{1}{n-1})$,
即 $\frac{1}{{(n-1){a_n}}}-\frac{1}{a_2}=-(1-\frac{1}{n-1}),n≥2$,
∴$\frac{1}{{(n-1){a_n}}}=\frac{1}{a_2}-(1-\frac{1}{n-1})=\frac{3n-2}{n-1}$,${a_n}=\frac{1}{3n-2},n≥2$.
又n=1時也成立,故${a_n}=\frac{1}{3n-2},n∈{N^*}$.
(Ⅱ)證明:當k≥2,有$a_k^2=\frac{1}{{{{(3k-2)}^2}}}<\frac{1}{(3k-4)(3k-1)}=\frac{1}{3}(\frac{1}{3k-4}-\frac{1}{3k-1})$,
∴n≥2時,有$\sum_{k=1}^n{a_k^2}=1+\sum_{k=2}^n{a_k^2}<1+\frac{1}{3}[{(\frac{1}{2}-\frac{1}{5})+(\frac{1}{5}-\frac{1}{8})+…+(\frac{1}{3n-4}-\frac{1}{3n-1})}]$=$1+\frac{1}{3}({\frac{1}{2}-\frac{1}{3n-1}})<1+\frac{1}{6}=\frac{7}{6}$.
又n=1時,$a_1^2=1<\frac{7}{6}$.
故對一切n∈N*,有$\sum_{k=1}^n{a_k^2}<\frac{7}{6}$.
點評 本題考查了“累加求和”、“裂項求和”方法、數列的單調性,考查了推理能力與計算能力,屬于難題.


科目:高中數學 來源: 題型:解答題
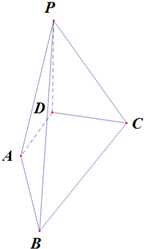 如圖,PD⊥平面ABCD,AD⊥DC,AD∥BC,PD:DC:BC=1:1:$\sqrt{2}$.
如圖,PD⊥平面ABCD,AD⊥DC,AD∥BC,PD:DC:BC=1:1:$\sqrt{2}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $-\sqrt{3}$ | C. | $±\frac{{\sqrt{3}}}{3}$ | D. | $-\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f(1)<f(-1)<c | B. | f(-1)<c<f(1) | C. | f(1)<c<f(3) | D. | c<f(3)<f(1) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 底面是矩形的平行六面體是長方體 | |
| B. | 底面是正方形的直平行六面體是正四棱柱 | |
| C. | 底面是正方形的直四棱柱是正方體 | |
| D. | 所有棱長都相等的直平行六面體是正方體 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 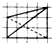 | B. | 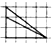 | C. | 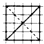 | D. |  |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com