
分析 (Ⅰ利潤函數為y=甲商品所得的利潤P+乙商品所得的利潤y=$\frac{3}{5}\sqrt{x}$+$\frac{1}{5}$(3-x),x∈[0,3].
(Ⅱ)y=$\frac{3}{5}\sqrt{x}$+$\frac{1}{5}$(3-x)=-$\frac{1}{5}(\sqrt{x}-\frac{3}{2})^{2}+\frac{21}{20}$.由二次函數的性質,得函數的最大值以及對應的x值.
解答 解:(Ⅰ)根據題意,得y=$\frac{3}{5}\sqrt{x}$+$\frac{1}{5}$(3-x),x∈[0,3].…(5分)
(Ⅱ)y=$\frac{3}{5}\sqrt{x}$+$\frac{1}{5}$(3-x)=-$\frac{1}{5}(\sqrt{x}-\frac{3}{2})^{2}+\frac{21}{20}$.
∵$\frac{3}{2}∈[0,3]$,∴當$\sqrt{x}$=$\frac{3}{2}$時,即x=$\frac{9}{4}$,3-x=$\frac{3}{4}$時,ymax=$\frac{21}{20}$.
即給甲、乙兩種商品分別投資$\frac{9}{4}$萬元、$\frac{3}{4}$萬元可使總利潤達到最大值$\frac{21}{20}$萬元.…(12分)
點評 本題考查了可化為二次函數模型的根式函數的應用,確定函數的解析式是關鍵,本題屬于基礎題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 若$\overrightarrow{b}$與$\overrightarrow{c}$不共線,則$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,$\overrightarrowp9vv5xb5$共面 | B. | 若$\overrightarrow{b}$與$\overrightarrow{c}$共線,則$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,$\overrightarrowp9vv5xb5$共面 | ||
| C. | 當且僅當$\overrightarrow{c}$=$\overrightarrow{0}$,$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,$\overrightarrowp9vv5xb5$共面 | D. | 若$\overrightarrow{b}$與$\overrightarrow{c}$不共線,則$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,$\overrightarrowp9vv5xb5$不共面 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {1,9} | B. | {0,1,9} | C. | {0} | D. | {0,2,4} |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
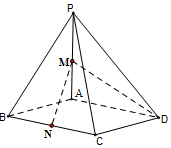 如圖,在四棱錐P-ABCD中,底面ABCD為菱形,∠ABC=$\frac{π}{3}$,PA⊥底面ABCD,PA=AB=2,M為PA的中點,N為BC的中點
如圖,在四棱錐P-ABCD中,底面ABCD為菱形,∠ABC=$\frac{π}{3}$,PA⊥底面ABCD,PA=AB=2,M為PA的中點,N為BC的中點查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com