
【題目】已知橢圓C:![]() 的左右焦點分別為F1、F2,過F1的直線交橢圓C與A、B兩點,△AF2B的周長為
的左右焦點分別為F1、F2,過F1的直線交橢圓C與A、B兩點,△AF2B的周長為![]() ,且橢圓C經過點
,且橢圓C經過點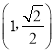 .
.
(1)求橢圓C的方程;
(2)當AB的中點坐標為![]() 時,求△AF2B的面積.
時,求△AF2B的面積.
【答案】(1)![]() y2=1(2)
y2=1(2)![]()
【解析】
(1)根據橢圓的定義求出a![]() ,再由橢圓上的點滿足橢圓方程求出
,再由橢圓上的點滿足橢圓方程求出![]() 即可.
即可.
(2)根據已知設出直線方程,將直線與橢圓聯立,利用中點弦公式求出直線方程,
再由弦長公式以及點到直線的距離即可求解.
(1)∵△AF2B的周長為4![]() ,故4a=4
,故4a=4![]() ,即a
,即a![]() ,
,
又橢圓經過點(1,![]() ),∴
),∴![]() 1,即b=1,
1,即b=1,
∴橢圓方程為![]() y2=1.
y2=1.
(2)由橢圓方程可知F1(﹣1,0),F2(1,0).
∵AB的中點(![]() ,
,![]() )在第二象限,顯然直線AB有斜率且斜率大于0,
)在第二象限,顯然直線AB有斜率且斜率大于0,
設直線AB的方程為y=k(x+1)(k>0),
代入橢圓方程可得:(![]() k2)x2+2k2x+k2﹣1=0,
k2)x2+2k2x+k2﹣1=0,
設A(x1,y1),B(x2,y2),即
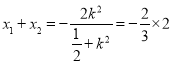 ,
,
解得:k=1,于是x1x2=0,
∴|AB|![]()
![]() .
.
又直線AB的方程為:y=x+1,F2(1,0),
∴F2到直線AB的距離d![]() ,
,
∴△ABF2的面積為![]() .
.


科目:高中數學 來源: 題型:
【題目】已知![]() ,
,![]() 是橢圓
是橢圓![]() :
:![]() 上的兩點,線段
上的兩點,線段![]() 的中點在直線
的中點在直線![]() 上.
上.
(1)當直線![]() 的斜率
的斜率![]() 存在時,求實數
存在時,求實數![]() 的取值范圍;
的取值范圍;
(2)設![]() 是橢圓
是橢圓![]() 的左焦點,若橢圓
的左焦點,若橢圓![]() 上存在一點
上存在一點![]() ,使
,使![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年8月8日是我國第十個全民健身日,其主題是:新時代全民健身動起來。某市為了解全民健身情況,隨機從某小區居民中抽取了40人,將他們的年齡分成7段:[10,20),[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]后得到如圖所示的頻率分布直方圖。

(1)試求這40人年齡的平均數、中位數的估計值;
(2)(i)若從樣本中年齡在[50,70)的居民中任取2人贈送健身卡,求這2人中至少有1人年齡不低于60歲的概率;
(ⅱ)已知該小區年齡在[10,80]內的總人數為2000,若18歲以上(含18歲)為成年人,試估計該小區年齡不超過80歲的成年人人數。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正方體![]() 的棱長為2,P是BC的中點,點Q是棱
的棱長為2,P是BC的中點,點Q是棱![]() 上的動點.
上的動點.
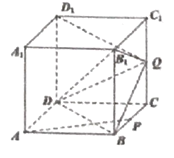
(1)點Q在何位置時,直線![]() ,DC,AP交于一點,并說明理由;
,DC,AP交于一點,并說明理由;
(2)求三棱錐![]() 的體積;
的體積;
(3)棱![]() 上是否存在動點Q,使得
上是否存在動點Q,使得![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ,若存在指出點Q在棱
,若存在指出點Q在棱![]() 上的位置,若不存在,請說明理由.
上的位置,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩品牌計劃入駐某商場,該商場批準兩個品牌先進場試銷![]() 天。兩品牌提供的返利方案如下:甲品牌無固定返利,賣出
天。兩品牌提供的返利方案如下:甲品牌無固定返利,賣出![]() 件以內(含
件以內(含![]() 件)的產品,每件產品返利
件)的產品,每件產品返利![]() 元,超出
元,超出![]() 件的部分每件返利
件的部分每件返利![]() 元;乙品牌每天固定返利
元;乙品牌每天固定返利![]() 元,且每賣出一件產品再返利
元,且每賣出一件產品再返利![]() 元。經統計,兩家品牌在試銷期間的銷售件數的莖葉圖如下:
元。經統計,兩家品牌在試銷期間的銷售件數的莖葉圖如下:
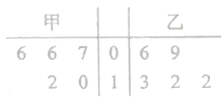
(Ⅰ)現從乙品牌試銷的![]() 天中隨機抽取
天中隨機抽取![]() 天,求這
天,求這![]() 天的銷售量中至少有一天低于
天的銷售量中至少有一天低于![]() 的概率.
的概率.
(Ⅱ)若將頻率視作概率,回答以下問題:
①記甲品牌的日返利額為![]() (單位:元),求
(單位:元),求![]() 的分布列和數學期望;
的分布列和數學期望;
②商場擬在甲、乙兩品牌中選擇一個長期銷售,如果僅從日返利額的角度考慮,請利用所學的統計學知識為商場作出選擇,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,在正方形![]() 中,
中,![]() 是
是![]() 的中點,點
的中點,點![]() 在線段
在線段![]() 上,且
上,且![]() .若將
.若將![]() 分別沿
分別沿![]() 折起,使
折起,使![]() 兩點重合于點
兩點重合于點![]() ,如圖2.
,如圖2.
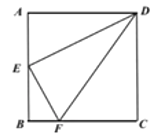
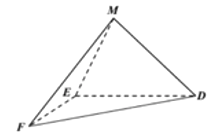
圖1 圖2
(1)求證:![]() 平面
平面![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,曲線![]() (α為參數)經過伸縮變換
(α為參數)經過伸縮變換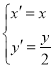 得到曲線C2.以坐標原點為極點,x軸正半軸為極軸建立極坐標系.
得到曲線C2.以坐標原點為極點,x軸正半軸為極軸建立極坐標系.
(1)求C2的普通方程;
(2)設曲線C3的極坐標方程為![]() ,且曲線C3與曲線C2相交于M,N兩點,點P(1,0),求
,且曲線C3與曲線C2相交于M,N兩點,點P(1,0),求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com