
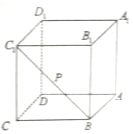
 如圖,點P是正方體ABCD-A1B1C1D1的面對角線BC1(線段BC1)上運動,給出下列五個命題:
如圖,點P是正方體ABCD-A1B1C1D1的面對角線BC1(線段BC1)上運動,給出下列五個命題:分析 對于①,根據異面直線的判定定理,可得結論;
對于②,連接A1B,A1C1容易證明平面BA1C1∥面ACD1,從而由線面平行的定義可得;
對于③,容易證明AD1∥BC1,從而BC1∥平面AD1C,以P為頂點,平面AD1C為底面,易得;
對于④,容易證明PDB1⊥面ACD1,從而可以證明面面垂直;
對于⑤,可以從向量的角度進行判斷;
解答 解:對于①:AD∥平面B1C1CB,B1P?平面B1C1CB,B1P與AD不平行,故直線AD與直線B1P為異面直線;①正確;
對于②:連接A1B,A1C1,可得平面BA1C1∥面ACD1,∵A1P?平面BA1C1,故A1P∥平面ACD1;②正確;
對于③:容易證明AD1∥BC1,從而BC1∥平面AD1C,故BC1上任意一點到平面AD1C的距離均相等,所以以P為頂點,平面AD1C為底面,則三棱錐A-D1PC的體積不變;③正確;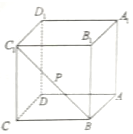
對于④:連接DB1,由DB1⊥AC且DB1⊥AD1,
可得DB1⊥面ACD1,從而由面面垂直的判定知,故④正確;
對于⑤:∵隨著P點的移動,$\overrightarrow{AP}$與平面ACD1的法向量的夾角也是變化的,∴⑤錯誤
故答案為:①②③④
點評 本題考查三棱錐體積求法中的等體積法;線面平行、垂直的判定,要注意使用轉化的思想.


科目:高中數學 來源: 題型:解答題
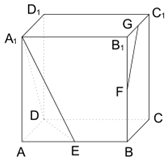 如 圖,正方體ABCD-A1B1C1D1的棱長為2,E、F、G 分別為 AB、BB1、B1C1 的中點.
如 圖,正方體ABCD-A1B1C1D1的棱長為2,E、F、G 分別為 AB、BB1、B1C1 的中點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
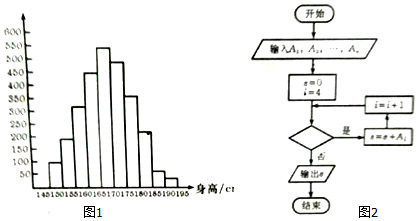
| A. | i<6 | B. | i<7 | C. | i<8 | D. | i<9 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [0,2] | B. | (0,2) | C. | (-∞,0)∪(2,+∞) | D. | (-∞,-2] |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-1)n-1$\frac{1}{{3}^{n}}$ | B. | (-1)n-1$\frac{1}{3n}$ | C. | (-1)n$\frac{1}{{3}^{n}}$ | D. | (-1)n$\frac{1}{3n}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{6}$ | B. | $\sqrt{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{6}}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
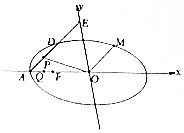 已知橢圓C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{12}$=1(a>2$\sqrt{3}$)的左焦點為F,左頂點為A,$\frac{1}{|OF|}$+$\frac{1}{|OA|}$=$\frac{3e}{|FA|}$,其中O為原點,e為橢圓的離心率,過點A作斜率為k(k≠0)的直線l交橢圓C于點D,交y軸于點E.
已知橢圓C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{12}$=1(a>2$\sqrt{3}$)的左焦點為F,左頂點為A,$\frac{1}{|OF|}$+$\frac{1}{|OA|}$=$\frac{3e}{|FA|}$,其中O為原點,e為橢圓的離心率,過點A作斜率為k(k≠0)的直線l交橢圓C于點D,交y軸于點E.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com