
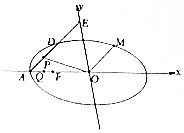
 已知橢圓C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{12}$=1(a>2$\sqrt{3}$)的左焦點(diǎn)為F,左頂點(diǎn)為A,$\frac{1}{|OF|}$+$\frac{1}{|OA|}$=$\frac{3e}{|FA|}$,其中O為原點(diǎn),e為橢圓的離心率,過(guò)點(diǎn)A作斜率為k(k≠0)的直線l交橢圓C于點(diǎn)D,交y軸于點(diǎn)E.
已知橢圓C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{12}$=1(a>2$\sqrt{3}$)的左焦點(diǎn)為F,左頂點(diǎn)為A,$\frac{1}{|OF|}$+$\frac{1}{|OA|}$=$\frac{3e}{|FA|}$,其中O為原點(diǎn),e為橢圓的離心率,過(guò)點(diǎn)A作斜率為k(k≠0)的直線l交橢圓C于點(diǎn)D,交y軸于點(diǎn)E.分析 (1)由$\frac{1}{|OF|}$+$\frac{1}{|OA|}$=$\frac{3e}{|FA|}$,可得:$\frac{1}{c}+\frac{1}{a}$=$\frac{3c}{a(a-c)}$,可得:a=2c,又a2=12+c2,解出即可得出.
(2)存在定值λ=$\frac{1}{2}$使得OP⊥EQ恒成立.下面給出分析:直線AD的方程為:y=k(x+4),則E(0,4k).直線方程與橢圓方程聯(lián)立化為:(3+4k2)x2+32k2x+64k2-48=0,利用根與系數(shù)的關(guān)系可得:D($\frac{12-16{k}^{2}}{3+4{k}^{2}}$,$\frac{24k}{3+4{k}^{2}}$),利用$\overrightarrow{AP}$=λ$\overrightarrow{AD}$,可得$\overrightarrow{OP}$=$\overrightarrow{OA}$+$λ\overrightarrow{AD}$.$\overrightarrow{EQ}$=(-3,-4k).假設(shè)$\overrightarrow{EQ}$⊥$\overrightarrow{OP}$,則$\overrightarrow{EQ}$•$\overrightarrow{OP}$=0,即可得出.
解答 解:(1)由$\frac{1}{|OF|}$+$\frac{1}{|OA|}$=$\frac{3e}{|FA|}$,可得:$\frac{1}{c}+\frac{1}{a}$=$\frac{3c}{a(a-c)}$,可得:a=2c,又a2=12+c2,解得a2=16,c=2.
∴橢圓C的方程為:$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}$=1.
(2)存在定值λ=$\frac{1}{2}$使得OP⊥EQ恒成立.下面給出證明:
直線AD的方程為:y=k(x+4),則E(0,4k).
聯(lián)立$\left\{\begin{array}{l}{y=k(x+4)}\\{\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1}\end{array}\right.$,化為:(3+4k2)x2+32k2x+64k2-48=0,
∴-4xD=$\frac{64{k}^{2}-48}{3+4{k}^{2}}$,解得xD=$\frac{12-16{k}^{2}}{3+4{k}^{2}}$,∴yD=$\frac{24k}{3+4{k}^{2}}$,∴D($\frac{12-16{k}^{2}}{3+4{k}^{2}}$,$\frac{24k}{3+4{k}^{2}}$),
∵$\overrightarrow{AP}$=λ$\overrightarrow{AD}$,可得$\overrightarrow{OP}$=$\overrightarrow{OA}$+$λ\overrightarrow{AD}$=$(\frac{24λ-12-16{k}^{2}}{3+4{k}^{2}},\frac{24λk}{3+4{k}^{2}})$.
$\overrightarrow{EQ}$=(-3,-4k).
假設(shè)$\overrightarrow{EQ}$⊥$\overrightarrow{OP}$,則$\overrightarrow{EQ}$•$\overrightarrow{OP}$=$\frac{-3(24λ-12-16{k}^{2})}{3+4{k}^{2}}$-$\frac{96λ{(lán)k}^{2}}{3+4{k}^{2}}$=0,
化為:(6+8k2)λ=3+4k2,解得λ=$\frac{1}{2}$.
因此存在定值λ=$\frac{1}{2}$使得OP⊥EQ恒成立.
點(diǎn)評(píng) 本題考查了橢圓的標(biāo)準(zhǔn)方程及其性質(zhì)、直線與橢圓相交問(wèn)題、一元二次方程的根與系數(shù)的關(guān)系、向量運(yùn)算性質(zhì)、向量垂直與數(shù)量積的關(guān)系,考查了推理能力與計(jì)算能力,屬于難題.


 閱讀快車(chē)系列答案
閱讀快車(chē)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
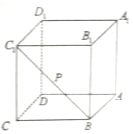 如圖,點(diǎn)P是正方體ABCD-A1B1C1D1的面對(duì)角線BC1(線段BC1)上運(yùn)動(dòng),給出下列五個(gè)命題:
如圖,點(diǎn)P是正方體ABCD-A1B1C1D1的面對(duì)角線BC1(線段BC1)上運(yùn)動(dòng),給出下列五個(gè)命題:查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
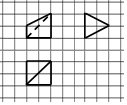 如圖,網(wǎng)格紙上小正方形的邊長(zhǎng)為1,粗實(shí)線及粗虛線畫(huà)出的是某多面體的三視圖,則該多面體外接球的表面積為( )
如圖,網(wǎng)格紙上小正方形的邊長(zhǎng)為1,粗實(shí)線及粗虛線畫(huà)出的是某多面體的三視圖,則該多面體外接球的表面積為( )| A. | 8π | B. | $\frac{25}{2}$π | C. | 12π | D. | $\frac{41}{4}$π |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 充分不必要條件 | B. | 必要不充分條件 | ||
| C. | 充要條件 | D. | 既不充分也不必要條件 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:填空題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com