
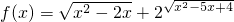 的最小值為1+2
的最小值為1+2 ;
; ,且|x1|>|x2|時,有f (x1)>f(x2)”是真命題;
,且|x1|>|x2|時,有f (x1)>f(x2)”是真命題;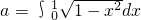 ”是函數“y=cos2(ax)-sin2(ax)的最小正周期為4”的充要條件;
”是函數“y=cos2(ax)-sin2(ax)的最小正周期為4”的充要條件; 為不共線向量,又
為不共線向量,又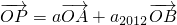 ,若
,若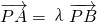 ,則S2012=2013.
,則S2012=2013.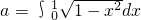 的值,及y=cos2(ax)-sin2(ax)的最小正周期為4時,對應的a值,比較后根據充要條件的定義可得答案;
的值,及y=cos2(ax)-sin2(ax)的最小正周期為4時,對應的a值,比較后根據充要條件的定義可得答案;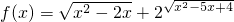 的定義域為{x|x≥4或x≤0}.
的定義域為{x|x≥4或x≤0}. ;
; ,
, <b,f (a)=2-a2,f (b)=b2-2,
<b,f (a)=2-a2,f (b)=b2-2, <b),
<b), ≤b)到直線4x+3y-15=0的距離的最小的點為(
≤b)到直線4x+3y-15=0的距離的最小的點為( ,
, )
) <b)不含(
<b)不含( ,
, )點
)點 上為增函數
上為增函數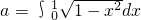 =
= ,則y=cos2(ax)-sin2(ax)的最小正周期為4,
,則y=cos2(ax)-sin2(ax)的最小正周期為4,
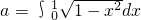 ”是函數“y=cos2(ax)-sin2(ax)的最小正周期為4”的充分不必要條件;
”是函數“y=cos2(ax)-sin2(ax)的最小正周期為4”的充分不必要條件;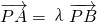 ,則P,A,B三點共線
,則P,A,B三點共線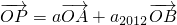 ,
,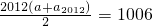 ≠2013
≠2013

科目:高中數學 來源: 題型:解答題
 =(1-tanx,1),
=(1-tanx,1), =(1+sin2x+cos2x,0),記f(x)=
=(1+sin2x+cos2x,0),記f(x)= •
• .
.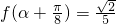 ,且
,且 ,求f(α).
,求f(α).查看答案和解析>>
科目:高中數學 來源: 題型:單選題
 =(6,1),
=(6,1), =(x,y),
=(x,y), =(-2,-3),則
=(-2,-3),則 等于
等于查看答案和解析>>
科目:高中數學 來源: 題型:解答題
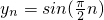 時,{yn}的周期為4的周期數列.
時,{yn}的周期為4的周期數列.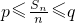 成立,若存在,求出p、q的取值范圍;不存在,說明理由.
成立,若存在,求出p、q的取值范圍;不存在,說明理由.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com