
分析 將函數f(x)表示為分段函數形式,①根據奇偶性的定義進行判斷,②利用周期性的定義進行排除,③結合三角函數的有界性進行求解,④求出函數的單調遞增區間進行判斷即可.
解答 解:當sinx≥0,即2kπ≤x≤2kπ+π,k∈Z,此時f(x)=sinx+cosx=$\sqrt{2}$sin(x+$\frac{π}{4}$),
當sinx<0,即2kπ-π≤x≤2kπ,k∈Z,此時f(x)=-sinx+cosx=$\sqrt{2}$cos(x+$\frac{π}{4}$),
①f(-x)=|sin(-x)|+cosx=|sinx|+cosx=f(x),則函數f(x)是偶函數,故①正確,
②f(x+$\frac{π}{2}$)=|sin(x+$\frac{π}{2}$)|+cos(x+$\frac{π}{2}$)=|cosx|-sinx≠f(x),則函數最小正周期為$\frac{π}{2}$錯誤,故②錯誤,
當2kπ≤x≤2kπ+π時,2kπ+$\frac{π}{4}$≤x+$\frac{π}{4}$≤2kπ+$\frac{5π}{4}$,此時$\sqrt{2}$sin(x+$\frac{π}{4}$)∈[-1,$\sqrt{2}$],
當2kπ-π≤x≤2kπ時,2kπ$-\frac{3π}{4}$≤x+$\frac{π}{4}$≤2kπ+$\frac{π}{4}$,此時$\sqrt{2}$cos(x+$\frac{π}{4}$)∈[-1,$\sqrt{2}$],
綜上f(x))∈[-1,$\sqrt{2}$],即函數的值域為[-1,$\sqrt{2}$],故③正確,
④作出函數f(x)的圖象如圖:函數單調遞增的最大區間在函數f(x)=$\sqrt{2}$cos(x+$\frac{π}{4}$),
由2kπ-π≤x+$\frac{π}{4}$≤2kπ,k∈Z得2kπ-$\frac{5π}{4}$≤x≤2kπ-$\frac{π}{4}$,k∈Z
∵2kπ-π≤x≤2kπ,∴此時2kπ-π≤x≤2kπ-$\frac{π}{4}$,即此時函數的單調遞增區間為[2kπ-π,2kπ-$\frac{π}{4}$],
當k=0時,單調遞增區間為[-π,-$\frac{π}{4}$],此時區間長度為-$\frac{π}{4}$-(-π)=$\frac{3π}{4}$,
故④正確,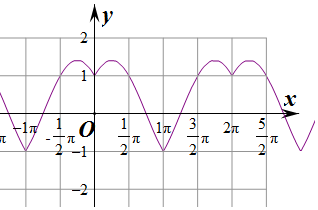
故答案為:①③④.
點評 本題主要考查與三角函數有關的命題的真假判斷,利用絕對值的性質將函數表示成分段函數是解決本題的關鍵.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,-1)∪(0,1) | B. | (-1,0)∪(1,+∞) | C. | (-1,0)∪(0,1) | D. | (-∞,-1)∪(1,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
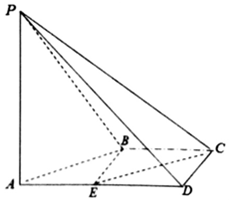 如圖,在四棱錐P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=$\frac{1}{2}$AD,E為AD的中點,異面直線AP與CD所成的角為90°.
如圖,在四棱錐P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=$\frac{1}{2}$AD,E為AD的中點,異面直線AP與CD所成的角為90°. 查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,四棱錐P-ABCD的一個側面PAD為等邊三角形,且平面PAD⊥平面ABCD,四邊形ABCD是平行四邊形,AD=2,AB=4,BD=2$\sqrt{3}$
如圖,四棱錐P-ABCD的一個側面PAD為等邊三角形,且平面PAD⊥平面ABCD,四邊形ABCD是平行四邊形,AD=2,AB=4,BD=2$\sqrt{3}$查看答案和解析>>
科目:高中數學 來源: 題型:解答題
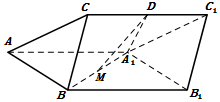 如圖,三棱柱ABC-A1B1C1中,側面ABB1A1為菱形且$∠BA{A_1}={60^o}$,D,M分別為CC1和A1B的中點,A1D⊥CC1,AA1=A1D=2,BC=1.
如圖,三棱柱ABC-A1B1C1中,側面ABB1A1為菱形且$∠BA{A_1}={60^o}$,D,M分別為CC1和A1B的中點,A1D⊥CC1,AA1=A1D=2,BC=1.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 4 | B. | 5 | C. | 6 | D. | $4+\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com