
【題目】已知f(x)=2ln(x+2)﹣(x+1)2 , g(x)=k(x+1).
(1)求f(x)的單調區間;
(2)當k=2時,求證:對于x>﹣1,f(x)<g(x)恒成立;
(3)若存在x0>﹣1,使得當x∈(﹣1,x0)時,恒有f(x)>g(x)成立,試求k的取值范圍.
【答案】
(1)解: ![]() ,
,
當f′(x)>0 時,所以 x2+3x+1<0,解得﹣2<x,
當f′(x)<0時,解得 ![]() ,
,
所以 f(x) 單調增區間為 ![]() ,遞減區間是(
,遞減區間是( ![]() ,+∞);
,+∞);
(2)解:當k=2時,g(x)=2(x+1).
令H(x)=f(x)﹣g(x)=2ln(x+2)﹣(x+1)2﹣2(x+1).
H′(x)= ![]() ,
,
令H′(x)=0,即﹣2x2﹣8x﹣6=0,解得x=﹣1或x=﹣3(舍).
∴當x>﹣1時,H′(x)<0,H(x)在(﹣1,+∞)上單調遞減.
∴Hmax(x)=H(﹣1)=0,
∴對于x>﹣1,H(x)<0,即f(x)<g(x).
(3)解:由(2)知,當k=2時,f (x)<g (x)恒成立,
即對于“x>﹣1,2 ln (x+2)﹣(x+1)2<2 (x+1),不存在滿足條件的x0;
當k>2時,對于“x>﹣1,x+1>0,此時2 (x+1)<k (x+1).
∴2 ln (x+2)﹣(x+1)2<2 (x+1)<k (x+1),
即f (x)<g (x)恒成立,不存在滿足條件的x0;
令h(x)=f(x)﹣g(x)=2ln(x+2)﹣(x+1)2﹣k(x+1),
h′(x)= ![]() ,
,
當k<2時,令t (x)=﹣2x2﹣(k+6)x﹣(2k+2),
可知t (x)與h′(x)符號相同,
當x∈(x0,+∞)時,t (x)<0,h′(x)<0,h (x)單調遞減,
當x∈(﹣1,x0)時,h (x)>h (﹣1)=0,即f (x)﹣g (x)>0恒成立,
綜上,k的取值范圍為(﹣∞,2)
【解析】(1)求出定義域和導數f′(x),令f′(x)>0,解出增區間,令f′(x)<0,解出減區間;(2)令H(x)=f(x)﹣g(x),利用導數判斷出H(x)的單調性和單調區間,得出H(x)的最大值,證明Hmax(x)<0即可.
【考點精析】解答此題的關鍵在于理解利用導數研究函數的單調性的相關知識,掌握一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減.
在這個區間單調遞減.


科目:高中數學 來源: 題型:
【題目】在△ABC中,內角A,B,C所對的邊分別為a,b,c.已知cos2A+ ![]() =2cosA.
=2cosA.
(1)求角A的大小;
(2)若a=1,求△ABC的周長l的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了調查某廠工人生產某種產品的能力,隨機抽查了20位工人某天生產該產品的數量.產品數量的分組區間為[45,55),[55,65),[65,75),[75,85),[85,95)由此得到頻率分布直方圖如圖.則產品數量位于[55,65)范圍內的頻率為;這20名工人中一天生產該產品數量在[55,75)的人數是 . 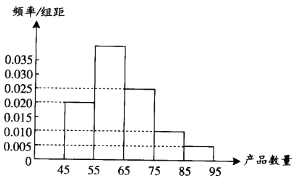
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=cosxsin(x+![]() )﹣
)﹣![]() cos2x+
cos2x+![]() ,x∈R.
,x∈R.
(1)求f(x)的單調遞增區間;
(2)在銳角△ABC中,角A,B,C的對邊分別a,b,c,若f(A)=![]() ,a=
,a=![]() ,求△ABC面積的最大值.
,求△ABC面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,半圓![]() 的直徑為
的直徑為![]() ,
, ![]() 為直徑延長線上的一點,
為直徑延長線上的一點, ![]() ,
, ![]() 為半圓上任意一點,以
為半圓上任意一點,以![]() 為一邊作等邊三角形
為一邊作等邊三角形![]() ,設
,設![]()
![]() .
.
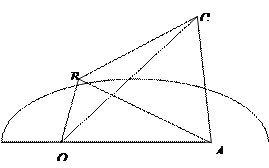
(1)當![]() 為何值時,四邊形
為何值時,四邊形![]() 面積最大,最大值為多少;
面積最大,最大值為多少;
(2)當![]() 為何值時,
為何值時, ![]() 長最大,最大值為多少.
長最大,最大值為多少.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 為正整數,數列
為正整數,數列![]() 滿足
滿足![]() ,
, ![]() ,設數列
,設數列![]() 滿足
滿足![]()
(1)求證:數列![]() 為等比數列;
為等比數列;
(2)若數列![]() 是等差數列,求實數
是等差數列,求實數![]() 的值;
的值;
(3)若數列![]() 是等差數列,前
是等差數列,前![]() 項和為
項和為![]() ,對任意的
,對任意的![]() ,均存在
,均存在![]() ,使得
,使得![]() 成立,求滿足條件的所有整數
成立,求滿足條件的所有整數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2018海南高三階段性測試(二模)】如圖,在直三棱柱![]() 中,
中, ![]() ,
, ![]() ,點
,點![]() 為
為![]() 的中點,點
的中點,點![]() 為
為![]() 上一動點.
上一動點.
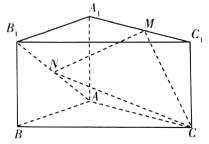
(I)是否存在一點![]() ,使得線段
,使得線段![]() 平面
平面![]() ?若存在,指出點
?若存在,指出點![]() 的位置,若不存在,請說明理由.
的位置,若不存在,請說明理由.
(II)若點![]() 為
為![]() 的中點且
的中點且![]() ,求三棱錐
,求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校舉辦校園科技文化藝術節,在同一時間安排《生活趣味數學》和《校園舞蹈賞析》兩場講座.已知A、B兩學習小組各有5位同學,每位同學在兩場講座任意選聽一場.若A組1人選聽《生活趣味數學》,其余4人選聽《校園舞蹈賞析》;B組2人選聽《生活趣味數學》,其余3人選聽《校園舞蹈賞析》.
(1)若從此10人中任意選出3人,求選出的3人中恰有2人選聽《校園舞蹈賞析》的概率;
(2)若從A、B兩組中各任選2人,設X為選出的4人中選聽《生活趣味數學》的人數,求X的分布列和數學期望E(X).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com