
【題目】已知![]() 為正整數,數列
為正整數,數列![]() 滿足
滿足![]() ,
, ![]() ,設數列
,設數列![]() 滿足
滿足![]()
(1)求證:數列![]() 為等比數列;
為等比數列;
(2)若數列![]() 是等差數列,求實數
是等差數列,求實數![]() 的值;
的值;
(3)若數列![]() 是等差數列,前
是等差數列,前![]() 項和為
項和為![]() ,對任意的
,對任意的![]() ,均存在
,均存在![]() ,使得
,使得![]() 成立,求滿足條件的所有整數
成立,求滿足條件的所有整數![]() 的值.
的值.
【答案】(1)見解析;(2)![]() ;(3)見解析.
;(3)見解析.
【解析】試題分析:
(1)由![]() ,可得
,可得![]() ,兩邊開方得
,兩邊開方得![]() ,于是證得數列
,于是證得數列![]() 為等比數列.(2)由(1)可得
為等比數列.(2)由(1)可得![]() ,故
,故![]() ,從而可得數列
,從而可得數列![]() 的通項公式,根據等差數列可得
的通項公式,根據等差數列可得![]() ,由此求得
,由此求得![]() 或
或![]() ,然后分別驗證可得
,然后分別驗證可得![]() 符合條件.(3)由題意可得有
符合條件.(3)由題意可得有![]() 成立,即
成立,即![]() 對任意的
對任意的![]() ,均存在
,均存在![]() 成立,且
成立,且![]() 為正整數,然后將
為正整數,然后將![]() 分為奇數和偶數兩種情況討論,最后可得
分為奇數和偶數兩種情況討論,最后可得![]() 時符合題意.
時符合題意.
試題解析:
(1)證明:∵![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() ,
,
![]() 數列
數列![]() 是首項為
是首項為![]() ,公比為2的等比數列.
,公比為2的等比數列.
(2)解:由(1)得![]() ,
,
∴![]() ,
,
∴![]()
![]() 數列
數列![]() 是等差數列,
是等差數列,
∴![]() ,
,
![]() ,
,
解得![]() 或
或![]() .
.
當![]() 時,
時,![]() ,是關于n的一次函數,因此數列
,是關于n的一次函數,因此數列![]() 是等差數列;
是等差數列;
當![]() 時,
時,![]() ,由于
,由于![]() ,不是常數,因此數列
,不是常數,因此數列![]() 不是等差數列.
不是等差數列.
綜上可得![]() .
.
(3)解:由(2)得![]() ,
,
對任意的![]() ,均存在
,均存在![]() ,使得
,使得![]() 成立,
成立,
即有![]() ,
,
化簡得![]() ,
,
當![]() 時,
時,![]() ,對任意的
,對任意的![]() ,符合題意;
,符合題意;
當![]() 時,若
時,若![]() ,則
,則![]() 不符合題意.對任意的
不符合題意.對任意的![]() ,也不符合題意.
,也不符合題意.
綜上可得,當![]() ,對任意的
,對任意的![]() ,均存在
,均存在![]() ,使得
,使得![]() 成立.
成立.


科目:高中數學 來源: 題型:
【題目】如圖,已知圓O外有一點P,作圓O的切線PM,M為切點,過PM的中點N,作割線NAB,交圓于A,B兩點,連接PA并延長,交圓O于點C,連續PB交圓O于點D,若MC=BC. 
(1)求證:△APM∽△ABP;
(2)求證:四邊形PMCD是平行四邊形.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)=2ln(x+2)﹣(x+1)2 , g(x)=k(x+1).
(1)求f(x)的單調區間;
(2)當k=2時,求證:對于x>﹣1,f(x)<g(x)恒成立;
(3)若存在x0>﹣1,使得當x∈(﹣1,x0)時,恒有f(x)>g(x)成立,試求k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了調查某廠工人生產某種產品的能力,隨機抽查了20位工人某天生產該產品的數量.產品數量的分組區間為[45,55),[55,65),[65,75),[75,85),[85,95)由此得到頻率分布直方圖如圖.則產品數量位于[55,65)范圍內的頻率為;這20名工人中一天生產該產品數量在[55,75)的人數是 . 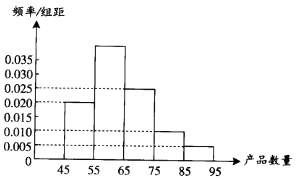
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知四邊形![]() 是正方形,
是正方形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 都是等邊三角形,
都是等邊三角形, ![]() 、
、![]() 、
、![]() 、
、![]() 分別是線段
分別是線段![]() 、
、![]() 、
、![]() 、
、![]() 的中點,分別以
的中點,分別以![]() 、
、![]() 、
、![]() 、
、![]() 為折痕將四個等邊三角形折起,使得
為折痕將四個等邊三角形折起,使得![]() 、
、![]() 、
、![]() 、
、![]() 四點重合于一點
四點重合于一點![]() ,得到一個四棱錐.對于下面四個結論:
,得到一個四棱錐.對于下面四個結論:
①![]() 與
與![]() 為異面直線; ②直線
為異面直線; ②直線![]() 與直線
與直線![]() 所成的角為
所成的角為![]()
③![]() 平面
平面![]() ; ④平面
; ④平面![]() 平面
平面![]() ;
;
其中正確結論的個數有( )

A. ![]() 個 B.
個 B. ![]() 個 C.
個 C. ![]() 個 D.
個 D. ![]() 個
個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,等邊三角形![]() 的中線
的中線![]() 與中位線
與中位線![]() 相交于
相交于![]() ,已知
,已知![]() 是
是![]() 繞
繞![]() 旋轉過程中的一個圖形,下列命題中,錯誤的是
旋轉過程中的一個圖形,下列命題中,錯誤的是

A. 恒有![]() ⊥
⊥![]()
B. 異面直線![]() 與
與![]() 不可能垂直
不可能垂直
C. 恒有平面![]() ⊥平面
⊥平面![]()
D. 動點![]() 在平面
在平面![]() 上的射影在線段
上的射影在線段![]() 上
上
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設{an}是公比大于1的等比數列,Sn為數列{an}的前n項和,已知S3=7,
且a1+3,3a2,a3+4構成等差數列.
(1)求數列{an}的通項;
(2)令![]() ,n=1,2,…,求數列{bn}的前n項和Tn .
,n=1,2,…,求數列{bn}的前n項和Tn .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com