
【題目】某市為調研學校師生的環境保護意識,決定在本市所有學校中隨機抽取60所進行環境綜合考評成績達到80分以上(含80分)為達標.60所學校的考評結果頻率分布直方圖如圖所示(其分組區間為[50,60),[60,70),[70,80),[80,90),[90,100]).

(Ⅰ)試根據樣本估汁全市學校環境綜合考評的達標率;
(Ⅱ)若考評成績在[90.100]內為優秀.且甲乙兩所學校考評結果均為優秀從考評結果為優秀的學校中隨機地抽取兩所學校作經驗交流報告,求甲乙兩所學校至少有一所被選中的概率.
【答案】(Ⅰ)0.35,(Ⅱ)甲乙兩所學校至少有所被選中的概率P=![]() .
.
【解析】
試題(Ⅰ)根據頻率分布直方圖,計算即可.
(Ⅱ)先求出參加考評結果均為優秀的學校有0.10×60=6所,求概率,要一一列舉出所有滿足條件的基本事件根據古典概型的問題求其答案.
解:(Ⅰ)由頻率分步直方圖得,考評分不低于80的頻率為:
1﹣0.05﹣0.2﹣0.4=0.35,
(Ⅱ)考評分在{90,100]的頻率為0.1
所以參加考評結果均為優秀的學校有0.10×60=6所,
又已知甲乙兩所學校考評結果均為優秀,
這6所學校分別記為:甲,乙,丙,丁,戊,己,故從中抽取2所共(甲乙),(甲丙),(甲丁),(甲戊),(甲己),(乙丙),(乙丁),(乙戊),(乙己),
(丙丁),(丙戊),(丙己),(丁戊),(丁己),(戊己)15種基本事件,
甲乙兩所學校至少有所被選中的有(甲乙),(甲丙),(甲丁),(甲戊),(甲己),(乙丙),(乙丁),(乙戊),(乙己)9種基本事件.
所以甲乙兩所學校至少有所被選中的概率P=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】過直線2x+y+4=0和圓x2+y2+2x﹣4y+1=0的交點,且面積最小的圓方程為( )
A.(x+![]() )2+(y+
)2+(y+![]() )2=
)2=![]() B.(x﹣
B.(x﹣![]() )2+(y﹣
)2+(y﹣![]() )2=
)2=![]()
C.(x﹣![]() )2+(y+
)2+(y+![]() )2=
)2=![]() D.(x+
D.(x+![]() )2+(y﹣
)2+(y﹣![]() )2=
)2=![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】過直線2x+y+4=0和圓x2+y2+2x﹣4y+1=0的交點,且面積最小的圓方程為( )
A.(x+![]() )2+(y+
)2+(y+![]() )2=
)2=![]() B.(x﹣
B.(x﹣![]() )2+(y﹣
)2+(y﹣![]() )2=
)2=![]()
C.(x﹣![]() )2+(y+
)2+(y+![]() )2=
)2=![]() D.(x+
D.(x+![]() )2+(y﹣
)2+(y﹣![]() )2=
)2=![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現代社會,“鼠標手”已成為常見病,一次實驗中,10名實驗對象進行160分鐘的連續鼠標點擊游戲,每位實驗對象完成的游戲關卡一樣,鼠標點擊頻率平均為180次/分鐘,實驗研究人員測試了實驗對象使用鼠標前后的握力變化,前臂表面肌電頻率(![]() )等指標.
)等指標.
(I)10 名實驗對象實驗前、后握力(單位:![]() )測試結果如下:
)測試結果如下:
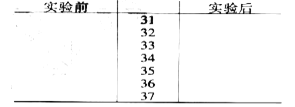
實驗前:346,357,358,360,362,362,364,372,373,376
實驗后:313,321,322,324,330,332,334,343,350,361
完成莖葉圖,并計算實驗后握力平均值比實驗前握力的平均值下降了多少![]() ?
?
(Ⅱ)實驗過程中測得時間![]() (分)與10名實驗對象前臂表面肌電頻率(
(分)與10名實驗對象前臂表面肌電頻率(![]() )的中的位數
)的中的位數![]() (
(![]() )的九組對應數據
)的九組對應數據![]() 為
為![]() ,
,![]() .建立
.建立![]() 關于時間
關于時間![]() 的線性回歸方程;
的線性回歸方程;
(Ⅲ)若肌肉肌電水平顯著下降,提示肌肉明顯進入疲勞狀態,根據(Ⅱ)中9組數據分析,使用鼠標多少分鐘就該進行休息了?
參考數據:![]() ;
;
參考公式:回歸方程![]() 中斜率和截距的最小二乘估計公式分別為:
中斜率和截距的最小二乘估計公式分別為:
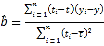 ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() (a>b>0)的左.右頂點分別為A,B,離心率為
(a>b>0)的左.右頂點分別為A,B,離心率為![]() ,點P
,點P![]() 為橢圓上一點.
為橢圓上一點.
(1) 求橢圓C的標準方程;
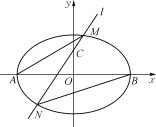
(2) 如圖,過點C(0,1)且斜率大于1的直線l與橢圓交于M,N兩點,記直線AM的斜率為k1,直線BN的斜率為k2,若k1=2k2,求直線l斜率的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大學生參加社會實踐活動,對某公司1月份至6月份銷售某種配件的銷售量及銷售單價進行了調查,銷售單價![]() 和銷售量
和銷售量![]() 之間的一組數據如下表所示:
之間的一組數據如下表所示:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
銷售單價 | 9 | 9.5 | 10 | 10.5 | 11 | 8 |
銷售量 | 11 | 10 | 8 | 6 | 5 | 14.2 |
(1)根據1至5月份的數據,先求出![]() 關于
關于![]() 的回歸直線方程;6月份的數據作為檢驗數據.若由回歸直線方程得到的預測數據與檢驗數據的誤差不超過
的回歸直線方程;6月份的數據作為檢驗數據.若由回歸直線方程得到的預測數據與檢驗數據的誤差不超過![]() ,則認為所得到的回歸直線方程是理想的.試問所求得的回歸直線方程是否理想?
,則認為所得到的回歸直線方程是理想的.試問所求得的回歸直線方程是否理想?
(2)預計在今后的銷售中,銷售量與銷售單價仍然服從(1)中的回歸關系,如果該種機器配件的成本是![]() 元/件,那么該配件的銷售單價應定為多少元才能獲得最大利潤?(注:利潤=銷售收入-成本).
元/件,那么該配件的銷售單價應定為多少元才能獲得最大利潤?(注:利潤=銷售收入-成本).
參考數據:![]() ,
,![]() .
.
參考公式:對于一組數據![]() ,
,![]() ,…,
,…,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: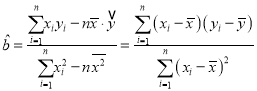 ,
,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com