
 如圖,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC⊥CB,點M和N分別是B1C1和BC的中點.
如圖,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC⊥CB,點M和N分別是B1C1和BC的中點.分析 (1)證明MC1NB為平行四邊形,所以C1N∥MB,即可證明MB∥平面AC1N;
(2)證明AC⊥平面BCC1B1,即可證明AC⊥MB.
解答 證明:(1)證明:在三棱柱ABC-A1B1C1中,因為點M,N分別是B1C1,BC的中點,
所以C1M∥BN,C1M=BN.
所以MC1NB為平行四邊形.
所以C1N∥MB.
因為C1N?平面AC1N,MB?平面AC1N,
所以MB∥平面AC1N;
(2)因為CC1⊥底面ABC,
所以AC⊥CC1.
因為AC⊥BC,BC∩CC1=C,
所以AC⊥平面BCC1B1.
因為MB?平面BCC1B1,
所以AC⊥MB.
點評 本題考查線面平行的判定,考查線面垂直的判定與性質,考查學生分析解決問題的能力,屬于中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 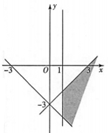 | B. | 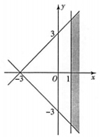 | C. | 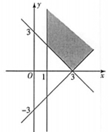 | D. | 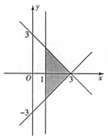 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
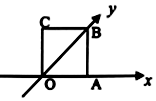 如圖水平放置的一個平面圖形的直觀圖是邊長為1cm的正方形,則原圖形的周長是( )
如圖水平放置的一個平面圖形的直觀圖是邊長為1cm的正方形,則原圖形的周長是( )| A. | 8cm | B. | 6cm | C. | $2(1+\sqrt{3})cm$ | D. | $2(1+\sqrt{2})cm$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$i | D. | -$\frac{1}{2}i$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (0,5) | B. | (5,10) | C. | (10,15) | D. | (15,20) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com