【題目】為了解某市的交通狀況，現對其6條道路進行評估，得分分別為：5,6,7,8,9,10.規定評估的平均得分與全市的總體交通狀況等級如下表：
評估的平均得分 |
|
|
|
全市的總體交通狀況等級 | 不合格 | 合格 | 優秀 |
（1）求本次評估的平均得分，并參照上表估計該市的總體交通狀況等級；
（2）用簡單隨機抽樣方法從這
條道路中抽取
條，它們的得分組成一個樣本，求該樣本的平均數與總體的平均數之差的絕對值不超過
的概率.
【答案】（1）7.5,合格（2）
【解析】
試題分析：（1）根據平均數計算公式得
，對照標準為合格.（2）求古典概型概率關鍵在于正確表示事件所包含基本事件數.作為文科用枚舉法進行列舉：從
條道路中抽取
條的得分組成的所有基本事件為：
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，共
個基本事件. 事件“樣本平均數與總體平均數之差的絕對值不超過
” 包括
，，，，，，共
個基本事件，因此該樣本平均數與總體平均數之差的絕對值不超過
的概率為.
試題解析：（1）6條道路的平均得分為. 3分
∴該市的總體交通狀況等級為合格. 5分
（2）設
表示事件“樣本平均數與總體平均數之差的絕對值不超過”. 7分
從條道路中抽取條的得分組成的所有基本事件為：，，，，，，，，，，，，，，，共個基本事件． 9分
事件
包括，，，，，，共個基本事件，
∴
．
答：該樣本平均數與總體平均數之差的絕對值不超過的概率為. 12分
科目：高中數學 來源： 題型：
【題目】已知冪函數y=f（x）的圖象過點 
．
（1）求函數f（x）的解析式
（2）記g（x）=f（x）+x ， 判斷g（x）在（1，+∞）上的單調性，并證明之．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某批發市場對某種商品的日銷售量（單位：噸）進行統計，最近50天的統計結果如下：
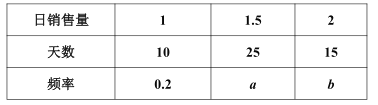
若以上表中頻率作為概率，且每天的銷售量相互獨立.
（1）求5天中該種商品恰好有兩天的日銷售量為1.5噸的概率；
（2）已知每噸該商品的銷售利潤為2千元， 
表示該種商品某兩天銷售利潤的和（單位：千元），求
的分布列和數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=x3+ax2+b滿足f（1）=0，且在x=2時函數取得極值．
（1）求a，b的值；
（2）求函數f（x）的單調區間；
（3）求函數f（x）在區間[0，t]（t＞0）上的最大值g（t）的表達式．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知拋物線
，直線
交
于
兩點， 
是
的中點，過
作
軸的垂線交
于
點.
（1）證明：拋物線
在
點處的切線與
平行；
（2）是否存在實數
，使以
為直徑的圓
經過
點？若存在，求出
的值；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】函數f（x）是定義在（﹣∞，0）∪（0，+∞）上的偶函數，當x＞0時， 
．
（1）求f（x）的解析式；
（2）討論函數f（x）的單調性，并求f（x）的值域．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）= 
在點（1，2）處的切線與f（x）的圖象有三個公共點，則b的取值范圍是（ ）
A.[﹣8，﹣4+2 
）
B.（﹣4﹣2 ，﹣4+2 ）
C.（﹣4+2 ，8]
D.（﹣4﹣2 ，﹣8]
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
