
分析 (1)捆綁法:把甲乙看成一個整體,再全排列即可,
(2)插空法:將甲乙插入到剩下3人排列后所成的間隔中,
(3)間接法:先求出沒有限制要求的,再排除有要求的,
直接法:分兩類,第一類,乙在中間,乙不在中間,
(4)定序法,甲乙丙的順序共3種,其中甲,乙均在丙的同側占$\frac{2}{3}$.
解答 解:(1)捆綁法:把甲乙看成一個整體,這樣5個人變成了4個人,全排列共有A22A44=48 (種)站法,
(2)插空法:因為甲、乙不相鄰,中間有隔檔,可用“插空法”,第一步先讓甲、乙以外的3個人站隊,有A33種;第二步再將甲、乙排在3人形成的4個空檔(含兩端)中,有A42種,故共有站法為A33A42=72(種).
(3)間接法:若對甲乙沒有限制條件共有A55種法,甲在中間有A44種站法,乙在兩端有2A44種,甲站中間乙站兩端的有2A33種,
故甲不站中間,乙不站兩端共有A55-3A44+2A33=120-72+12=60,
直接法:第一類,乙在中間,有A44=24種,乙不在中間,有A21A31A33=36種,根據分類計數原理共有24+36=60種,
(4)定序法:甲,乙均在丙的同側,甲乙丙的順序共3種,其中甲,乙均在丙的同側占$\frac{2}{3}$,故有$\frac{2}{3}$A55=80種.
點評 本題主要考查排列組合的實際應用,本題解題的關鍵是對于有限制的元素要優先排,特殊位置要優先排.相鄰的問題用捆綁法,不相鄰的問題用插空法,體現了分類討論的數學思想,是一個中檔題目


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\frac{2}{5}$ | B. | -$\frac{2}{5}$ | C. | 5 | D. | -$\sqrt{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{3}$ | D. | $\frac{7}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{3}{4}$ | B. | $\frac{{2\sqrt{2}}}{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{{2\sqrt{6}}}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題

| A. | $8+2\sqrt{5}$ | B. | $6+2\sqrt{5}$ | C. | $8+2\sqrt{3}$ | D. | $6+2\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
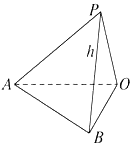 如圖所示,在地面上有一旗桿OP,為測得它的高度h,在地面上取一線段AB,
如圖所示,在地面上有一旗桿OP,為測得它的高度h,在地面上取一線段AB,查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com