
分析 (1)利用三種方程的互化方法,即可寫出曲線C1的極坐標方程與曲線C2的直角坐標方程;
(2)$A({ρ_1},θ),B({ρ_2},θ+\frac{π}{2})$分別代入$\frac{{{ρ^2}{{cos}^2}θ}}{4}+{ρ^2}{sin^2}θ=1$中,即可求$\frac{1}{{{{|{OA}|}^2}}}+\frac{1}{{{{|{OB}|}^2}}}$的值.
解答 解:(1)$\left\{\begin{array}{l}1=acos\frac{π}{3}\\ y=bsin\frac{π}{3}\end{array}\right.⇒\left\{\begin{array}{l}a=2\\ b=1\end{array}\right.⇒{C_1}:\frac{x^2}{4}+{y^2}=1$
因此C1的極坐標方程為$\frac{{{ρ^2}{{cos}^2}θ}}{4}+{ρ^2}{sin^2}θ=1$${C_2}:{x^2}+{y^2}=2y$
(2)M1(0,1),M2(2,0)⇒M1M2:x+2y-2=0
恰好過${C_2}:{x^2}+{y^2}=2y$的圓心,∴OP⊥OQ⇒OA⊥OB,
∴$A({ρ_1},θ),B({ρ_2},θ+\frac{π}{2})$
分別代入$\frac{{{ρ^2}{{cos}^2}θ}}{4}+{ρ^2}{sin^2}θ=1$中,
∴$\frac{1}{{{{|{OA}|}^2}}}+\frac{1}{{{{|{OB}|}^2}}}=\frac{1}{ρ_1^2}+\frac{1}{ρ_2^2}=\frac{{{{cos}^2}θ}}{4}+{sin^2}θ+\frac{{{{sin}^2}θ}}{4}+{cos^2}θ=\frac{5}{4}$.
點評 本題考查三種方程的互化,考查極坐標方程的運用,屬于中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | 1 | C. | $\frac{1}{16}$ | D. | $\frac{1}{32}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
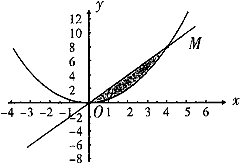 設曲線x2=2y與過原點的直線相交于點M,若直線OM的傾斜角為θ,則線段OM與曲線圍成的封閉圖形的面積S(θ)的圖象大致是( )
設曲線x2=2y與過原點的直線相交于點M,若直線OM的傾斜角為θ,則線段OM與曲線圍成的封閉圖形的面積S(θ)的圖象大致是( )| A. | 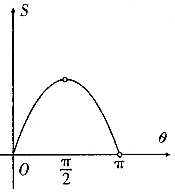 | B. | 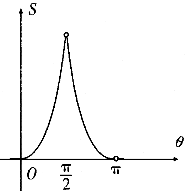 | ||
| C. | 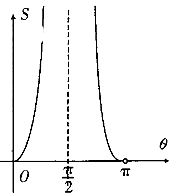 | D. | 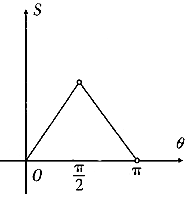 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
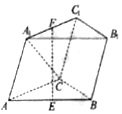 如圖,三棱柱ABC-A1B1C1中,側面AA1C1C⊥底面ACB,AA1=A1C=AC=2$\sqrt{3}$,BC=$\sqrt{3}$,且A1C⊥BC,點E,F分別為AB,A1C1的中點.
如圖,三棱柱ABC-A1B1C1中,側面AA1C1C⊥底面ACB,AA1=A1C=AC=2$\sqrt{3}$,BC=$\sqrt{3}$,且A1C⊥BC,點E,F分別為AB,A1C1的中點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com