
 如圖,在長方體ABCD-A1B1C1D1中,點E在棱CC1的延長線上,且CC1=C1E=BC=$\frac{1}{2}$AB=1.
如圖,在長方體ABCD-A1B1C1D1中,點E在棱CC1的延長線上,且CC1=C1E=BC=$\frac{1}{2}$AB=1.分析 (1)連接AD1、BC1,可得四邊形AB1ED1是平行四邊形,即D1E∥平面ACB1,可得點F到平面ACB1的距離等于點E到平面ACB1的距離,由${V_{E-AC{B_1}}}={V_{A-{B_1}CE}}$,得D1E的中點F到平面ACB1的距離.
(2)由已知得,${B_1}{C^2}+{B_1}{E^2}=4=C{E^2}$,則B1E⊥B1C,CD⊥B1E,即B1E⊥平面DCB1,又B1E?平面D1B1E,即可得平面D1B1E⊥平面DCB1.
解答  證明:(1)連接AD1、BC1,∵$A{D_1}\underline{\underline{∥}}B{C_1}\underline{\underline{∥}}{B_1}E$,
證明:(1)連接AD1、BC1,∵$A{D_1}\underline{\underline{∥}}B{C_1}\underline{\underline{∥}}{B_1}E$,
∴四邊形AB1ED1是平行四邊形,
∴D1E∥AB1,又AB1?平面AB1C,D1E?平面AB1C,
∴D1E∥平面ACB1,
∴點F到平面ACB1的距離等于點E到平面ACB1的距離,由${V_{E-AC{B_1}}}={V_{A-{B_1}CE}}$,
得$\frac{1}{3}{S_{△AC{B_1}}}•h=\frac{1}{3}×\frac{1}{2}×1×2×2$,又易知${S_{△AC{B_1}}}=\frac{3}{2}$.
∴D1E的中點F到平面ACB1的距離為$h=\frac{4}{3}$.
(2)由已知得,${B_1}{C^2}+{B_1}{E^2}=4=C{E^2}$,則B1E⊥B1C,
由長方體的特征可知CD⊥平面B1BCE,
而B1E?平面B1BCE,所以CD⊥B1E,
∴B1E⊥平面DCB1,又B1E?平面D1B1E,
∴平面D1B1E⊥平面DCB1.
點評 本題考查了空間線面、面面位置關系,點面距離,屬于中檔題.


 陽光課堂同步練習系列答案
陽光課堂同步練習系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}+\frac{1}{2}i$ | B. | $\frac{1}{2}-\frac{1}{2}i$ | C. | $-\frac{1}{2}+\frac{1}{2}i$ | D. | $-\frac{1}{2}-\frac{1}{2}i$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {x|1≤x<2} | B. | {x|x>2} | C. | {x|x≥1或x<0} | D. | {x|x>0} |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
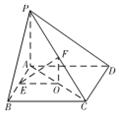 如圖,四棱錐中P-ABCD,PA⊥平面ABCD,∠PDA=30°,O,E,F分別是AC,AB,PC的中點.
如圖,四棱錐中P-ABCD,PA⊥平面ABCD,∠PDA=30°,O,E,F分別是AC,AB,PC的中點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com