
【題目】已知橢圓![]() :
:![]() (
(![]() )過點
)過點![]() 與
與![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設過橢圓![]() 的右焦點
的右焦點![]() ,且傾斜角為
,且傾斜角為![]() 的直線
的直線![]() 和橢圓
和橢圓![]() 交于
交于![]() 、
、![]() 兩點,對于橢圓
兩點,對于橢圓![]() 上任一點
上任一點![]() ,若
,若![]() ,求
,求![]() 的最大值.
的最大值.
 探究與鞏固河南科學技術出版社系列答案
探究與鞏固河南科學技術出版社系列答案科目:高中數學 來源: 題型:
【題目】請你設計一個包裝盒,如圖所示,ABCD是邊長為60cm的正方形硬紙片,切去陰影部分所示的四個全等的等腰直角三角形,再沿虛線折起,使得![]() 四個點重合于圖中的點P,正好形成一個正四棱柱形狀的包裝盒,E、F在AB上是被切去的等腰直角三角形斜邊的兩個端點,設AE=FB=xcm2
四個點重合于圖中的點P,正好形成一個正四棱柱形狀的包裝盒,E、F在AB上是被切去的等腰直角三角形斜邊的兩個端點,設AE=FB=xcm2
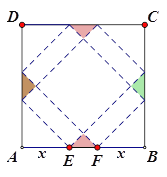
(1)若廣告商要求包裝盒側面積S(cm![]() )最大,試問x應取何值?
)最大,試問x應取何值?
(2)若廣告商要求包裝盒容積V(cm![]() )最大,試問x應取何值?并求出此時包裝盒的高與底面邊長的比值。
)最大,試問x應取何值?并求出此時包裝盒的高與底面邊長的比值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】謝賓斯基三角形是一種分形,由波蘭數學家謝賓斯基在1915年提出,先作一個正三角形.挖去一個“中心三角形”(即以原三角形各邊的中點為頂點的三角形),然后在剩下的小三角形中又挖去一個“中心三角形”,我們用白色代表挖去的面積,那么黑三角形為剩下的面積(我們稱黑三角形為謝賓斯基三角形).向圖中第5個大正三角形中隨機撒512粒大小均勻的細小顆粒物,則落在白色區域的細小顆粒物的數量約是( )

A.256B.350C.162D.96
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于數列![]() 、
、![]() ,把和
,把和![]() 叫做數列
叫做數列![]() 與
與![]() 的前
的前![]() 項泛和,記作為
項泛和,記作為![]() .已知數列
.已知數列![]() 的前
的前![]() 項和為
項和為![]() ,且
,且![]() .
.
(1)求數列![]() 的通項公式;
的通項公式;
(2)數列![]() 與數列
與數列![]() 的前
的前![]() 項的泛和為
項的泛和為![]() ,且
,且![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(3)從數列![]() 的前
的前![]() 項中,任取
項中,任取![]() 項從小到大依次排列,得到數列
項從小到大依次排列,得到數列![]() 、
、![]() 、
、![]() 、
、![]() ;再將余下的
;再將余下的![]() 項從大到小依次排列,得到數列
項從大到小依次排列,得到數列![]() 、
、![]() 、
、![]() 、
、![]() .求數列
.求數列![]() 與數列
與數列![]() 的前
的前![]() 項的泛和
項的泛和![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 是定義在R上的奇函數,當
是定義在R上的奇函數,當![]() 時,
時,![]() ,給出下列命題:
,給出下列命題:
①當![]() 時,
時,![]() ;
;
②函數![]() 有2個零點;
有2個零點;
③![]() 的解集為
的解集為![]() ;
;
④![]() ,
,![]() ,都有
,都有![]() .
.
其中真命題的個數為( )
A.4B.3C.2D.1
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com