
【題目】關于函數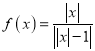 ,給出以下四個命題,其中真命題的序號是_______.
,給出以下四個命題,其中真命題的序號是_______.
①![]() 時,
時,![]() 單調遞減且沒有最值;
單調遞減且沒有最值;
②方程![]() 一定有解;
一定有解;
③如果方程![]() 有解,則解的個數一定是偶數;
有解,則解的個數一定是偶數;
④![]() 是偶函數且有最小值.
是偶函數且有最小值.
【答案】②④
【解析】
①將函數![]() 表示為分段函數,結合分式型函數的單調性進行判斷;②由函數
表示為分段函數,結合分式型函數的單調性進行判斷;②由函數![]() 是偶函數,在
是偶函數,在![]() 且
且![]() 時,判定函數
時,判定函數![]() 與函數
與函數![]() 在
在![]() 時有唯一交點,同理得出,當
時有唯一交點,同理得出,當![]() 且
且![]() 時,函數
時,函數![]() 與函數
與函數![]() 在
在![]() 時有交點,從而可得方程
時有交點,從而可得方程![]() 有解;③求方程
有解;③求方程![]() 的解,即可判斷出命題③的正誤;④利用偶函數的定義判定函數
的解,即可判斷出命題③的正誤;④利用偶函數的定義判定函數![]() 為偶函數,再利用絕對值的性質得出
為偶函數,再利用絕對值的性質得出![]() 且
且![]() ,即可判斷出命題④的正誤.
,即可判斷出命題④的正誤.
對于命題①,當![]() 時,
時,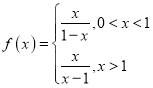 .
.
當![]() 時,
時,![]() ,則函數
,則函數![]() 在
在![]() 上單調遞增,此時,
上單調遞增,此時,![]() ,當
,當![]() 時,
時,![]() ,
,
當![]() 時,
時,![]() ,則函數
,則函數![]() 在
在![]() 上單調遞減,
上單調遞減,
所以,當![]() 時,函數
時,函數![]() 不單調且沒有最值,命題①錯誤;
不單調且沒有最值,命題①錯誤;
對于命題②,當![]() 時,
時,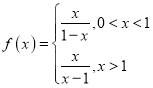 ,當
,當![]() 時,
時,![]() ,
,
當![]() 時,構造函數
時,構造函數![]() ,
,
則函數![]() 在
在![]() 上單調遞增,
上單調遞增,
當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() ,
,
所以,函數![]() 在
在![]() 上有且只有一個零點,
上有且只有一個零點,
即當![]() 時,方程
時,方程![]() 在
在![]() 上有解.
上有解.
函數![]() 的定義域為
的定義域為![]() ,關于原點對稱,
,關于原點對稱, ,則函數
,則函數![]() 為偶函數,
為偶函數,
同理可知,當![]() 時,方程
時,方程![]() 在
在![]() 上有解.
上有解.
所以,命題②正確;
對于命題③,當![]() 時,令
時,令![]() ,解得
,解得![]() ,則命題③錯誤;
,則命題③錯誤;
對于命題④,由②可知,函數![]() 是偶函數,由絕對值的性質可知
是偶函數,由絕對值的性質可知![]() 且
且![]() ,則函數
,則函數![]() 為偶函數且最小值為
為偶函數且最小值為![]() ,命題④正確.
,命題④正確.
因此,正確命題的序號為②④.
故答案為:②④.


科目:高中數學 來源: 題型:
【題目】已知a,b,c分別為△ABC三個內角A,B,C的對邊,且acos C+![]() asin C-b-c=0.
asin C-b-c=0.
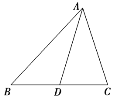
(1)求A;
(2)若AD為BC邊上的中線,cos B=![]() ,AD=
,AD=![]() ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數![]() 與
與![]() 在給定的區間上滿足
在給定的區間上滿足![]() 恒成立,則稱這兩個函數在該區間上“和諧”。
恒成立,則稱這兩個函數在該區間上“和諧”。
(1)若函數![]() 與
與![]() 在R上和諧,求實數a的取值范圍;
在R上和諧,求實數a的取值范圍;
(2)若函數![]() 與
與![]() 在
在![]() 上和諧,求實數a的取值范圍.
上和諧,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合![]() ,集合
,集合![]() ,集合
,集合![]() .
.
(1)用列舉法表示集合C;
(2)設集合C的含n個元素所有子集為![]() ,記有限集合M的所有元素和為
,記有限集合M的所有元素和為![]() ,求
,求![]()
![]() 的值;
的值;
(3)已知集合P、Q是集合C的兩個不同子集,若P不是Q的子集,且Q不是P的子集,求所有不同的有序集合對![]() 的個數
的個數![]() ;
;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“割圓術”是劉徽最突出的數學成就之一,他在《九章算術注》中提出割圓術,并作為計算圓的周長,面積已經圓周率的基礎,劉徽把圓內接正多邊形的面積一直算到了正3072邊形,并由此而求得了圓周率為3.1415和3.1416這兩個近似數值,這個結果是當時世界上圓周率計算的最精確數據.如圖,當分割到圓內接正六邊形時,某同學利用計算機隨機模擬法向圓內隨機投擲點,計算得出該點落在正六邊形內的頻率為0.8269,那么通過該實驗計算出來的圓周率近似值為(參考數據:![]() )
)

A. 3.1419B. 3.1417C. 3.1415D. 3.1413
查看答案和解析>>
科目:高中數學 來源: 題型:
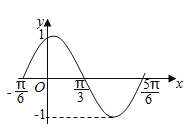
【題目】如圖是函數![]() 在區間
在區間![]() 上的圖象,為了得到這個函數的圖象,只需將
上的圖象,為了得到這個函數的圖象,只需將![]() 的圖象上的所有的點( )
的圖象上的所有的點( )
![]()
A.向左平移![]() 個長度單位,再把所得各點的橫坐標變為原來的
個長度單位,再把所得各點的橫坐標變為原來的![]() ,縱坐標不變
,縱坐標不變
B.向左平移![]() 個長度單位,再把所得各點的橫坐標變為原來的2倍,縱坐標不變
個長度單位,再把所得各點的橫坐標變為原來的2倍,縱坐標不變
C.向左平移![]() 個長度單位,再把所得各點的橫坐標變為原來的
個長度單位,再把所得各點的橫坐標變為原來的![]() ,縱坐標不變
,縱坐標不變
D.向左平移![]() 個長度單位,再把所得各點的橫坐標變為原來的2倍,縱坐標不變
個長度單位,再把所得各點的橫坐標變為原來的2倍,縱坐標不變
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2018湖北七市(州)教研協作體3月高三聯考】已知橢圓![]() :
: ![]()
![]() 的左頂點為
的左頂點為![]() ,上頂點為
,上頂點為![]() ,直線
,直線![]() 與直線
與直線![]() 垂直,垂足為
垂直,垂足為![]() 點,且點
點,且點![]() 是線段
是線段![]() 的中點.
的中點.
(I)求橢圓![]() 的方程;
的方程;
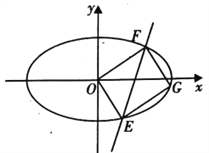
(II)如圖,若直線![]() :
: ![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
, ![]() 兩點,點
兩點,點![]() 在橢圓
在橢圓![]() 上,且四邊形
上,且四邊形![]() 為平行四邊形,求證:四邊形
為平行四邊形,求證:四邊形![]() 的面積
的面積![]() 為定值.
為定值.
【答案】(I)![]() ;(II)
;(II)![]()
【解析】試題分析:(1)根據題意可得![]() ,
, ![]() 故斜率為
故斜率為![]() ,由直線
,由直線![]() 與直線
與直線![]() 垂直,可得
垂直,可得![]() ,因為點
,因為點![]() 是線段
是線段![]() 的中點,∴點
的中點,∴點![]() 的坐標是
的坐標是![]() ,
,
代入直線得![]() ,連立方程即可得
,連立方程即可得![]() ,
, ![]() ;(2)∵四邊形
;(2)∵四邊形![]() 為平行四邊形,∴
為平行四邊形,∴![]() ,設
,設![]() ,
, ![]() ,
, ![]() ,∴
,∴![]()
![]() ,得
,得![]() ,將
,將![]() 點坐標代入橢圓
點坐標代入橢圓![]() 方程得
方程得![]() ,
,
點![]() 到直線
到直線![]() 的距離為
的距離為![]() ,利用弦長公式得EF,則平行四邊形
,利用弦長公式得EF,則平行四邊形![]() 的面積為
的面積為
![]()
![]()
![]()
![]()
![]()
![]() .
.
解析:(1)由題意知,橢圓![]() 的左頂點
的左頂點![]() ,上頂點
,上頂點![]() ,直線
,直線![]() 的斜率
的斜率![]() ,
,
得![]() ,
,
因為點![]() 是線段
是線段![]() 的中點,∴點
的中點,∴點![]() 的坐標是
的坐標是![]() ,
,
由點![]() 在直線
在直線![]() 上,∴
上,∴![]() ,且
,且![]() ,
,
解得![]() ,
, ![]() ,
,
∴橢圓![]() 的方程為
的方程為![]() .
.
(2)設![]() ,
, ![]() ,
, ![]() ,
,
將![]() 代入
代入![]() 消去
消去![]() 并整理得
并整理得![]()
![]() ,
,
則![]() ,
, ![]() ,
,
![]()
![]() ,
,
∵四邊形![]() 為平行四邊形,∴
為平行四邊形,∴![]()
![]() ,
,
得![]() ,將
,將![]() 點坐標代入橢圓
點坐標代入橢圓![]() 方程得
方程得![]() ,
,
點![]() 到直線
到直線![]() 的距離為
的距離為![]() ,
, ![]() ,
,
∴平行四邊形![]() 的面積為
的面積為
![]()
![]()
![]()
![]()
![]()
![]() .
.
故平行四邊形![]() 的面積
的面積![]() 為定值
為定值![]() .
.
【題型】解答題
【結束】
21
【題目】已知函數![]() ,
, ![]() .
.
(1)當![]() 時,討論函數
時,討論函數![]() 的單調性;
的單調性;
(2)當![]() 時,求證:函數
時,求證:函數![]() 有兩個不相等的零點
有兩個不相等的零點![]() ,
, ![]() ,且
,且![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的焦距與短軸長相等,長軸長為
的焦距與短軸長相等,長軸長為![]() ,設過右焦點F傾斜角為
,設過右焦點F傾斜角為![]() 的直線交橢圓M于A、B兩點.
的直線交橢圓M于A、B兩點.
(1)求橢圓M的方程;
(2)求證:![]()
(3)設過右焦點F且與直線AB垂直的直線交橢圓M于C、D,求四邊形ABCD面積的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com