
【題目】已知a,b,c分別為△ABC三個內角A,B,C的對邊,且acos C+![]() asin C-b-c=0.
asin C-b-c=0.
(1)求A;
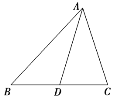
(2)若AD為BC邊上的中線,cos B=![]() ,AD=
,AD=![]() ,求△ABC的面積.
,求△ABC的面積.
【答案】(1)A=60°;(2)![]()
【解析】
(1)利用正弦定理,把邊化為角,結合輔助角公式可求;
(2)利用三角形內角關系求出![]() ,結合正弦定理求出
,結合正弦定理求出![]() 關系,利用余弦定理可求
關系,利用余弦定理可求![]() .
.
(1)acos C+![]() asin C-b-c=0,由正弦定理得sin Acos C+
asin C-b-c=0,由正弦定理得sin Acos C+![]() sin Asin C=sin B+sin C,
sin Asin C=sin B+sin C,
即sin Acos C+![]() sin Asin C=sin(A+C)+sin C,
sin Asin C=sin(A+C)+sin C,
又sin C≠0,所以化簡得![]() sin A-cos A=1,所以sin(A-30°)=
sin A-cos A=1,所以sin(A-30°)=![]() .
.
在△ABC中,0°<A<180°,所以A-30°=30°,得A=60°.
(2)在△ABC中,因為cos B=![]() ,所以sin B=
,所以sin B=![]() .
.
所以sin C=sin(A+B)=![]() ×
×![]() +
+![]() ×
×![]() =
=![]() .
.
由正弦定理得,![]() .
.
設a=7x,c=5x(x>0),則在△ABD中,AD2=AB2+BD2-2AB·BDcos B,
即![]() =25x2+
=25x2+![]() ×49x2-2×5x×
×49x2-2×5x×![]() ×7x×
×7x×![]() ,解得x=1,所以a=7,c=5,
,解得x=1,所以a=7,c=5,
故S△ABC=![]() acsin B=10
acsin B=10![]() .
.


 新課標快樂提優暑假作業陜西旅游出版社系列答案
新課標快樂提優暑假作業陜西旅游出版社系列答案科目:高中數學 來源: 題型:
【題目】已知數列![]() 中,
中,![]() ,
,![]() ,
,![]() 的前
的前![]() 項和為
項和為![]() ,且滿足
,且滿足![]() (
(![]() ).
).
(1)試求數列![]() 的通項公式;
的通項公式;
(2)令![]() ,
,![]() 是
是![]() 的前
的前![]() 項和,證明:
項和,證明:![]() ;
;
(3)證明:對任意給定的![]() ,均存在
,均存在![]() ,使得
,使得![]() 時,(2)中的
時,(2)中的![]() 恒成立.
恒成立.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某油庫的設計容量為30萬噸,年初儲量為10萬噸,從年初起計劃每月購進石油![]() 萬噸,以滿足區域內和區域外的需求,若區域內每月用石油1萬噸,區域外前
萬噸,以滿足區域內和區域外的需求,若區域內每月用石油1萬噸,區域外前![]() 個月的需求量
個月的需求量![]() (萬噸)與
(萬噸)與![]() 的函數關系為
的函數關系為![]() ,并且前4個月區域外的需求量為20萬噸.
,并且前4個月區域外的需求量為20萬噸.
(1)試寫出第![]() 個月石油調出后,油庫內儲油量
個月石油調出后,油庫內儲油量![]() (萬噸)與
(萬噸)與![]() 的函數關系式;
的函數關系式;
(2)要使16個月內每月按計劃購進石油之后,油庫總能滿足區域內和區域外的需求,且每月石油調出后,油庫的石油剩余量不超出油庫的容量,試確定![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知各項均為正數的數列![]() 的前
的前![]() 項和為
項和為![]() 且滿足:
且滿足:![]()
(1)求數列![]() 的通項公式;
的通項公式;
(2)設![]() 求
求![]() 的值;
的值;
(3)是否存在大于2的正整數![]() 使得
使得![]() ?若存在,求出所有符合條件的
?若存在,求出所有符合條件的![]() 若不存在,請說明理由.
若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的兩個焦點分別為
的兩個焦點分別為![]() ,長軸長為
,長軸長為![]() .
.
(Ⅰ)求橢圓![]() 的標準方程及離心率;
的標準方程及離心率;
(Ⅱ)過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
,![]() 兩點,若點
兩點,若點![]() 滿足
滿足![]() ,求證:由點
,求證:由點![]() 構成的曲線
構成的曲線![]() 關于直線
關于直線![]() 對稱.
對稱.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 、
、![]() 為橢圓
為橢圓![]() (
(![]() )和雙曲線
)和雙曲線![]() 的公共頂點,
的公共頂點,![]() 、
、![]() 分為雙曲線和橢圓上不同于
分為雙曲線和橢圓上不同于![]() 、
、![]() 的動點,且滿足
的動點,且滿足![]() ,設直線
,設直線![]() 、
、![]() 、
、![]() 、
、![]() 的斜率分別為
的斜率分別為![]() 、
、![]() 、
、![]() 、
、![]() .
.
(1)求證:點![]() 、
、![]() 、
、![]() 三點共線;
三點共線;
(2)求![]() 的值;
的值;
(3)若![]() 、
、![]() 分別為橢圓和雙曲線的右焦點,且
分別為橢圓和雙曲線的右焦點,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有以下命題:
①若函數f(x)既是奇函數又是偶函數,則f(x)的值域為{0};
②若函數f(x)是偶函數,則f(|x|)=f(x);
③若函數f(x)在其定義域內不是單調函數,則f(x)不存在反函數;
④若函數f(x)存在反函數f﹣1(x),且f﹣1(x)與f(x)不完全相同,則f(x)與f﹣1(x)圖象的公共點必在直線y=x上;
其中真命題的序號是 .(寫出所有真命題的序號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】關于函數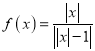 ,給出以下四個命題,其中真命題的序號是_______.
,給出以下四個命題,其中真命題的序號是_______.
①![]() 時,
時,![]() 單調遞減且沒有最值;
單調遞減且沒有最值;
②方程![]() 一定有解;
一定有解;
③如果方程![]() 有解,則解的個數一定是偶數;
有解,則解的個數一定是偶數;
④![]() 是偶函數且有最小值.
是偶函數且有最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com