
分析 當n>2,且n∈N時,f(n)<g(n),利用數學歸納法,可證得結論.
解答 解:當n>2,且n∈N時,f(n)<g(n),證明如下:
當n=3時,f(n)=$1+\frac{1}{\sqrt{1}}+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}$,$g(n)=2\sqrt{3}$,f(n)<g(n)成立,
假定n=k(k>2,且k∈N)時,f(k)<g(k)成立,
即$1+\frac{1}{\sqrt{1}}+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+…+\frac{1}{\sqrt{k}}$<2$\sqrt{k}$,
則當n=k+1時,$1+\frac{1}{\sqrt{1}}+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+…+\frac{1}{\sqrt{k}}$+$\frac{1}{\sqrt{k+1}}$<2$\sqrt{k}$+$\frac{1}{\sqrt{k+1}}$
∵(k+$\frac{1}{2}$)2=k2+k+$\frac{1}{4}$>k2+k,
∴$\sqrt{{k}^{2}+k}$<k+$\frac{1}{2}$,
∴2$\sqrt{{k}^{2}+k}$<2k+1,
∴2$\sqrt{{k}^{2}+k}$+1<2(k+1),
∴2$\sqrt{k}$+$\frac{1}{\sqrt{k+1}}$<2$\sqrt{k+1}$,
即$1+\frac{1}{\sqrt{1}}+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+…+\frac{1}{\sqrt{k}}$+$\frac{1}{\sqrt{k+1}}$<2$\sqrt{k+1}$,
綜上可得:當n>2,且n∈N時,f(n)<g(n)恒成立.
點評 本題考查的知識點是不等式的證明,數學歸納法,難度中檔.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 向右平移$\frac{π}{8}$ | B. | 向左平移$\frac{π}{8}$ | C. | 向右平移$\frac{π}{4}$ | D. | 向左平移$\frac{π}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
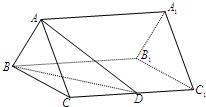 如圖,已知正三棱柱ABC-A1B1C1的底面邊長是2,D是側棱CC1的中點,直線AD與側BB1C1C所成的角為45°.
如圖,已知正三棱柱ABC-A1B1C1的底面邊長是2,D是側棱CC1的中點,直線AD與側BB1C1C所成的角為45°.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,四棱錐P-ABCD中,PB⊥底面ABCD.底面ABCD為直角梯形,∠ABC=90°,AD∥BC,BC=2,AB=AD=PB=1,點E為棱PA的中點.
如圖,四棱錐P-ABCD中,PB⊥底面ABCD.底面ABCD為直角梯形,∠ABC=90°,AD∥BC,BC=2,AB=AD=PB=1,點E為棱PA的中點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com