
【題目】物業公司為了改善某小區空氣質量和居住環境,計劃將小區內部的空地種植綠植,平時許多用戶將私家車停在空地上,為了了解該小區居民對種植綠植的態度,在該小區中隨機抽查了100人進行了調查,調查情況如下表:
年齡段 |
|
|
|
|
|
|
頻數 | 5 | 15 | 20 |
| 20 | 10 |
贊成人數 | 3 | 12 | 17 | 18 | 16 | 2 |
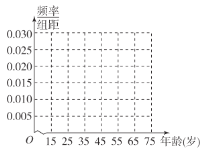
(1)求出表格中![]() 的值,并完成被調查人員年齡的頻率分布圖.
的值,并完成被調查人員年齡的頻率分布圖.
(2)若從年齡在![]() 被調查者中按照是否贊成進行分層抽樣,從中抽取5人參與某項調查,然后再從這5人中隨機抽取2人參加座談會,求選出的2人中至少有1人贊成“種植綠植”的概率.
被調查者中按照是否贊成進行分層抽樣,從中抽取5人參與某項調查,然后再從這5人中隨機抽取2人參加座談會,求選出的2人中至少有1人贊成“種植綠植”的概率.
【答案】(1)![]() ,見解析(2)
,見解析(2)![]()
【解析】
(1)由樣本容量求出![]() 的值,填寫頻率分布表,即可畫出頻率分布直方圖;
的值,填寫頻率分布表,即可畫出頻率分布直方圖;
(2)由(1)知,年齡在![]() 的共有30人,其中贊成的有18人,不贊成的有12人,利用分層抽樣求出抽取的5人中贊成者人數為3人,不贊成人數為2人,一一列出基本事件,根據古典概型即可求出概率.
的共有30人,其中贊成的有18人,不贊成的有12人,利用分層抽樣求出抽取的5人中贊成者人數為3人,不贊成人數為2人,一一列出基本事件,根據古典概型即可求出概率.
解:(1)由題知被調查者一共100人,
所以有![]() ,
,
解得:![]() ,
,
則被調查人員年齡各組的頻率為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以頻率分布表如下:
年齡段 |
|
|
|
|
|
|
頻數 | 5 | 15 | 20 | 30 | 20 | 10 |
頻率 | 0.05 | 0.15 | 0.20 | 0.30 | 0.20 | 0.10 |
頻率/組距 | 0.005 | 0.015 | 0.020 | 0.030 | 0.020 | 0.010 |
所以被調查人員年齡的頻率分布直方圖如下圖所示:

(2)由(1)知,年齡在![]() 的共有30人,其中贊成的有18人,不贊成的有12人,
的共有30人,其中贊成的有18人,不贊成的有12人,
由分層抽樣贊成者應選![]() 人,記為
人,記為![]() ,
,![]() ,
,![]() ;不贊成有2人,記為
;不贊成有2人,記為![]() ,
,![]() ,
,
從中選取2人,不同的取法有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共10種,
,共10種,
其中至少有1人贊成的取法有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,共9種,
,共9種,
故選出的2人中至少有1人贊成“種植綠植”的概率為![]() .
.


科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() 的最大值為
的最大值為![]() .
.
(Ⅰ)求實數![]() 的值;
的值;
(Ⅱ)當![]() 時,討論函數
時,討論函數![]() 的單調性;
的單調性;
(Ⅲ)當![]() 時,令
時,令![]() ,是否存在區間
,是否存在區間![]() .使得函數
.使得函數![]() 在區間
在區間![]() 上的值域為
上的值域為![]() 若存在,求實數
若存在,求實數![]() 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2021年起,新高考科目設置采用“![]() ”模式,普通高中學生從高一升高二時將面臨著選擇物理還是歷史的問題,某校抽取了部分男、女學生調查選科意向,制作出如右圖等高條形圖,現給出下列結論:
”模式,普通高中學生從高一升高二時將面臨著選擇物理還是歷史的問題,某校抽取了部分男、女學生調查選科意向,制作出如右圖等高條形圖,現給出下列結論:
①樣本中的女生更傾向于選歷史;
②樣本中的男生更傾向于選物理;
③樣本中的男生和女生數量一樣多;
④樣本中意向物理的學生數量多于意向歷史的學生數量.
根據兩幅條形圖的信息,可以判斷上述結論正確的有( )


A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某電子元件生產廠家新引進一條產品質量檢測線,現對檢測線進行上線的檢測試驗:從裝有![]() 個正品和
個正品和![]() 個次品的同批次電子元件的盒子中隨機抽取出
個次品的同批次電子元件的盒子中隨機抽取出![]() 個,再將電子元件放回.重復
個,再將電子元件放回.重復![]() 次這樣的試驗,那么“取出的
次這樣的試驗,那么“取出的![]() 個電子元件中有
個電子元件中有![]() 個正品,
個正品,![]() 個次品”的結果恰好發生
個次品”的結果恰好發生![]() 次的概率是( )
次的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠只生產口罩、抽紙和棉簽,如圖是該工廠![]() 年至
年至![]() 年各產量的百分比堆積圖(例如:
年各產量的百分比堆積圖(例如:![]() 年該工廠口罩、抽紙、棉簽產量分別占
年該工廠口罩、抽紙、棉簽產量分別占![]() 、
、![]() 、
、![]() ),根據該圖,以下結論一定正確的是( )
),根據該圖,以下結論一定正確的是( )
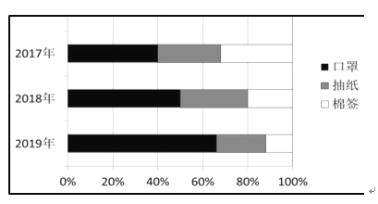
A.![]() 年該工廠的棉簽產量最少
年該工廠的棉簽產量最少
B.這三年中每年抽紙的產量相差不明顯
C.三年累計下來產量最多的是口罩
D.口罩的產量逐年增加
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com