
分析 根據條件分別構造函數g(x)=$\frac{f(x)}{{x}^{9}}$和h(x)=$\frac{f(x)}{{x}^{10}}$,分別求函數的導數,研究函數的單調性進行求解即可.
解答 解:設g(x)=$\frac{f(x)}{{x}^{9}}$,
∴g′(x)=$\frac{f′(x){x}^{9}-f(x)9{x}^{8}}{({x}^{9})^{2}}$=$\frac{xf′(x)-9f(x)}{{x}^{10}}$,
∵9f(x)<xf'(x),
∴g′(x)=$\frac{xf′(x)-9f(x)}{{x}^{10}}$>0,
即g(x)在(0,+∞)上是增函數,
則g(2)>g(1),
即$\frac{f(2)}{{2}^{9}}$>$\frac{f(1)}{{1}^{9}}$,則$\frac{f(2)}{f(1)}$>29,
同理設h(x)=$\frac{f(x)}{{x}^{10}}$,
∴h′(x)=$\frac{f′(x){x}^{10}-f(x)•10{x}^{9}}{({x}^{10})^{2}}$=$\frac{xf′(x)-10f(x)}{{x}^{11}}$,
∵xf'(x)<10f(x),
∴h′(x)=$\frac{xf′(x)-10f(x)}{{x}^{11}}$<0,
即h(x)在(0,+∞)上是減函數,
則h(2)<h(1),
即$\frac{f(2)}{{2}^{10}}$<$\frac{f(1)}{{1}^{10}}$,則$\frac{f(2)}{f(1)}$<210,
綜上29<$\frac{f(2)}{f(1)}$<210,
故答案為:(29,210)
點評 本題主要考查函數取值范圍的求解,根據條件分別構造兩個函數,利用函數單調性和導數之間的關系進行轉化是解決本題的關鍵.


科目:高中數學 來源: 題型:選擇題
| A. | S2015=2 015,a1009>1>a1007 | B. | S2015=2 015,a1007>1>a1009 | ||
| C. | S2015=-2 015,a1009>1>a1007 | D. | S2015=-2 015,a1007>1>a1009 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{5}{4}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 6 | B. | -4 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
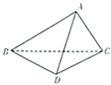 如圖,三棱錐A-BCD中,DC⊥BD,BC=2$\sqrt{3}$,CD=AC=2,AB=AD=2$\sqrt{2}$.
如圖,三棱錐A-BCD中,DC⊥BD,BC=2$\sqrt{3}$,CD=AC=2,AB=AD=2$\sqrt{2}$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | $\frac{7}{12}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com