Question

函數y=x²+1（0≤x≤1）圖象上點P處的切線與直線y=0，x=0，x=1圍成的梯形面積等于S，則S的最大值等于    ，此時點P的坐標是    ．

Answer 1

【答案】分析：設P點坐標為（a，a²+1）則得到在P處的切線方程，利用定積分的方法求出梯形的面積，求出面積的最大值即可得到P的坐標．
解答：解：設P（a，a²+1）則過P的切線方程為：y=2ax-a²+1
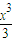
則S=∫¹（2ax-a²-1）dx=（3x--x²）|¹=-a²+a+1為二次函數，
當a=時，S有最大值，S_max=．且此時P的坐標為（，）．
故答案為，（，）
點評：考查學生會利用導數求切線斜率并寫出切線方程的能力，以及會利用定積分求圖形面積的能力．