
【題目】對某電子元件進行壽命追蹤調查,所得情況如右頻率分布直方圖.
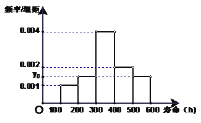
(1)圖中縱坐標![]() 處刻度不清,根據圖表所提供的數據還原
處刻度不清,根據圖表所提供的數據還原![]() ;
;
(2)根據圖表的數據按分層抽樣,抽取![]() 個元件,壽命為
個元件,壽命為![]() 之間的應抽取幾個;
之間的應抽取幾個;
(3)從(2)中抽出的壽命落在![]() 之間的元件中任取
之間的元件中任取![]() 個元件,求事件“恰好有一個壽命為
個元件,求事件“恰好有一個壽命為![]() ,一個壽命為
,一個壽命為![]() ”的概率.
”的概率.
【答案】(1)![]() ;(2)應抽取
;(2)應抽取![]() 個;(3)
個;(3)![]() .
.
【解析】
試題分析:(1)根據題意:![]() ,即可求得
,即可求得![]() 的值;(2)設在壽命為
的值;(2)設在壽命為![]() 之間的應抽取
之間的應抽取![]() 個,根據分層抽樣有:
個,根據分層抽樣有:![]() ,即可求解壽命為
,即可求解壽命為![]() 之間的應抽取幾個;(3)記“恰好有一個壽命為
之間的應抽取幾個;(3)記“恰好有一個壽命為![]() ,一個壽命為
,一個壽命為![]() ”為事件
”為事件![]() ,由(2)知壽命落在
,由(2)知壽命落在![]() 之間的元件有
之間的元件有![]() 個分別記
個分別記![]() ,落在
,落在![]() 之間的元件有
之間的元件有![]() 個分別記為:
個分別記為:![]() ,從中任取
,從中任取![]() 個球,即可利用古典概型求解概率.
個球,即可利用古典概型求解概率.
試題解析:(1)根據題意:![]()
解得![]()
(2)設在壽命為![]() 之間的應抽取
之間的應抽取![]() 個,根據分層抽樣有:
個,根據分層抽樣有:
![]()
解得:![]() 所以應在壽命為
所以應在壽命為![]() 之間的應抽取
之間的應抽取![]() 個
個
(3)記“恰好有一個壽命為![]() ,一個壽命為
,一個壽命為![]() ”為事件
”為事件![]() ,
,
由(2)知壽命落在![]() 之間的元件有
之間的元件有![]() 個分別記
個分別記![]() ,落在
,落在![]() 之間的元件有
之間的元件有![]() 個分別記為:
個分別記為:![]() ,從中任取
,從中任取![]() 個球,有如下基本事件:
個球,有如下基本事件:
![]() ,
,![]() ,
,
![]() ,共有
,共有![]() 個基本事件
個基本事件
事件![]() “恰好有一個壽命為
“恰好有一個壽命為![]() ,一個壽命為
,一個壽命為![]() ”有:
”有:
![]() ,
,![]() 共有
共有![]() 個基本事件
個基本事件
![]()
答:事件“恰好有一個壽命為![]() ,另一個壽命為
,另一個壽命為![]() ”的概率為
”的概率為![]() .
.


 中考解讀考點精練系列答案
中考解讀考點精練系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知曲線
中,已知曲線![]() (
(![]() 為參數),以平面直角坐標系
為參數),以平面直角坐標系![]() 的原點
的原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸,取相同的單位長度建立極坐標系,已知直線
軸的正半軸為極軸,取相同的單位長度建立極坐標系,已知直線![]() .
.
(1)將曲線![]() 上的所有點的橫坐標、縱坐標分別伸長為原來的
上的所有點的橫坐標、縱坐標分別伸長為原來的![]() ,2倍后得到曲線
,2倍后得到曲線![]() ,試寫出直線
,試寫出直線![]() 的直角坐標方程和曲線
的直角坐標方程和曲線![]() 的參數方程;
的參數方程;
(2)在曲線![]() 上求一點
上求一點![]() ,使點
,使點![]() 到直線
到直線![]() 的距離最大,并求出此最大值.
的距離最大,并求出此最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 的方程為
的方程為![]() .
.
(I)若點![]() 在圓
在圓![]() 的外部,求
的外部,求![]() 的取值范圍;
的取值范圍;
(II)當![]() 時,是否存在斜率為
時,是否存在斜率為![]() 的直線
的直線![]() ,使以
,使以![]() 被圓
被圓![]() 截得的弦
截得的弦![]() 為直徑所作的圓過原點?若存在,求出
為直徑所作的圓過原點?若存在,求出![]() 的方程;若不存在,說明理由.
的方程;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】平面內有兩個定點A(1,0),B(1,﹣2),設點P到A、B的距離分別為![]() ,且
,且![]()
(I)求點P的軌跡C的方程;
(II)是否存在過點A的直線![]() 與軌跡C相交于E、F兩點,滿足
與軌跡C相交于E、F兩點,滿足![]() (O為坐標原點).若存在,求出直線
(O為坐標原點).若存在,求出直線![]() 的方程;若不存在,請說明理由.
的方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】宜昌一中江南新校區擬建一個扇環形狀的花壇(如圖所示),按設計要求扇環的周長為30米,其中大圓弧所在圓的半徑為10米,設小圓弧所在圓的半徑為![]() 米,圓心角
米,圓心角![]() (弧度).
(弧度).
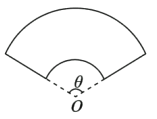
(1)求![]() 關于
關于![]() 的函數關系式;
的函數關系式;
(2)已知對花壇的邊緣(實線部分)進行裝飾時,直線部分的裝飾費用為4元/米,弧線部分的裝飾費用為9元/米,設花壇的面積與裝飾總費用之比為![]() ,求
,求![]() 關于
關于![]() 的函數關系式,并求出
的函數關系式,并求出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的前n項為和Sn,點(n,![]() )在直線y=
)在直線y=![]() x+
x+![]() 上.數列{bn}滿足bn+2-2bn+1+bn=0(nN*),且b3=11,前9項和為153.
上.數列{bn}滿足bn+2-2bn+1+bn=0(nN*),且b3=11,前9項和為153.
(1)求數列{an},{bn}的通項公式;
(2)求數列![]() 的前
的前![]() 項和
項和![]()
(3)設nN*,f(n)=![]() 問是否存在mN*,使得f(m+15)=5f(m)成立?若存在,求出m的值;若不存在,請說明理由.
問是否存在mN*,使得f(m+15)=5f(m)成立?若存在,求出m的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在發生某公共衛生事件期間,有專業機構認為該事件在一段時間沒有發生在規模群體感染的標志為“連續10天,每天新增疑似病例不超過7人”。根據過去10天甲、乙、丙、丁四地新增疑似病例數據,一定符合該標志的是 ( )
A. 甲地:總體均值為3,中位數為4
B. 乙地:總體均值為1,總體方差大于0
C. 丙地:中位數為2,眾數為3
D. 丁地:總體均值為2,總體方差為3
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com