
分析 (1)利用極坐標(biāo)方程與直角坐標(biāo)方程互化的方法,可得結(jié)論;
(2)利用參數(shù)方程,結(jié)合三角函數(shù)知識,求PQ中點M到曲線C2上的點的距離的最小值.
解答 解:(1)$ρ=\frac{3}{{cos(θ+\frac{π}{3})}}$,得$\frac{1}{2}ρcosθ-\frac{{\sqrt{3}}}{2}ρsinθ=3$,
故曲線C2的直角坐標(biāo)方程為$x-\sqrt{3}y-6=0$,
點Q的直角坐標(biāo)為(4,4).
(2)設(shè)P(12cosθ,4sinθ),故PQ中點M(2+6cosθ,2+2sinθ),C2的直線方程為$x-\sqrt{3}y-6=0$,
點M到C2的距離$d=\frac{{|2+6cosθ-\sqrt{3}(2+2sinθ)-6|}}{2}$=$|3cosθ-\sqrt{3}sinθ-2-\sqrt{3}|$
=$|2\sqrt{3}cos(θ+\frac{π}{6})-2-\sqrt{3}|≥|2\sqrt{3}-2-\sqrt{3}|=2-\sqrt{3}$,
PQ中點M到曲線C2上的點的距離的最小值是$2-\sqrt{3}$.
點評 本題考查極坐標(biāo)方程與直角坐標(biāo)方程互化,考查參數(shù)方程的運用,屬于中檔題.


 活力課時同步練習(xí)冊系列答案
活力課時同步練習(xí)冊系列答案科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
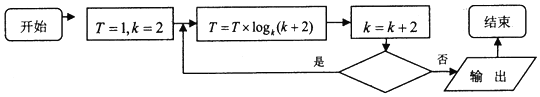
| A. | k<32 | B. | k<33 | C. | k<64 | D. | k<65 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\frac{9}{2}$ | B. | $\frac{{3\sqrt{2}}}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
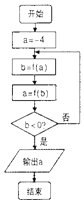
| A. | -3 | B. | $\frac{1}{16}$ | C. | $\frac{1}{4}$ | D. | 4 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com